
如图10,从⊙O外一点A作⊙O的切线AB、AC,切点分别为B、C,且⊙O的直经BD=6,连结CD、AO、BC,且AO与BC相交于点E。
(1)求证:CD∥AO;
(2)设CD=x,AO=y,求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(3)请阅读下方资源链接内容。
在(2)的基础上,若CD、AO的长
分别为一元二次方程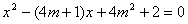 的两个实数根,求AB的长。
的两个实数根,求AB的长。
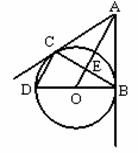
(1)证明:连接OC
∵AB、AC是⊙O的切线,∴∠ACO=∠ABO=90°
∵OC=OB,∴由HL可得 Rt△ACO≌Rt△ABO,∴AB=AC, ∠1=∠2
∴AE⊥BC, ∴∠AEC=90°
∵BD是⊙O的直径,∴∠DCB=90°, ∴∠DCB=∠AEC, ∴CD∥AO
(2)解:∵CD∥AO, ∴∠3=∠4
∵AB是⊙O的切线,DB是直径,∴∠DCB=∠ABO=90°
∴△BDC∽△AOB ∴ =
=  , ∴
, ∴ =
= , ∴y =
, ∴y = 
∵ ,∴自变量
,∴自变量 的取值范围为0<x<6 (3)解:∵CD、AO的长分别为一元二次方程
的取值范围为0<x<6 (3)解:∵CD、AO的长分别为一元二次方程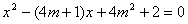 的两个实数根
的两个实数根
由求根公式可得,两根积为 ,
,
∴
又由(2)知y =  ,∴
,∴ ,∴
,∴ ,∴
,∴
①当 时,原方程可化为
时,原方程可化为 ,∴
,∴
由(2)知 ,∴只能取
,∴只能取
∴CD=3,AO=6,∴AB=
②当 时,原方程可化为
时,原方程可化为 ,
,
∵ ,∴方程无解
,∴方程无解
综上:AB的长为


科目:初中数学 来源: 题型:
为落实 校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.
校园“阳光体育”工程,某校计划购买篮球和排球共20个.已知篮球每个80元,排球每个60元.设购买篮球x个,购买篮球和排球的总费用y元.
(1)求y与x之间的函数关系式;
(2)如果要求篮球的个数不少于排球个数的3倍,应如何购买,才能使总费用最少?最少费用是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
近期随着国家抑制房价新政策的出台,某楼盘房价连续两次下跌,由原来的每平方米10000元降至每平方米8100元,设每次降价的百分率相同,则降价百分率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
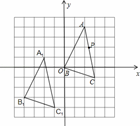
在如图所示的单位正方形网格中,△ABC经过平移后得到△A1B1C1,已知在AC上一点P(2.4,2)平移后的对应点为P1,点P1绕点O逆时针旋转180°,得到对应点P2,则P2点的坐标为( )
A.(1.4,﹣1) B.(1.5,2) C.(1.6,1) D.(2.4,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数 的图象上,则y1、y2、y3的大小关系是( )
的图象上,则y1、y2、y3的大小关系是( )
A.y3<y1<y2 B.y1<y2<y3 C.y2<y1<y3 D.y3<y2<y1
查看答案和解析>>
科目:初中数学 来源: 题型:
随着我国公民收入的提高,人们越来越关注健康的话题.关于甲醛污染问题也一直困扰人们.我国质检总局规定:针织内衣、被套、床上用品等直接接触皮肤的制品,每千克的衣物上甲醛含量应在0.000 075千克以下,将0.000 075用科学记数法表示为( )
A. 0.75×10﹣4 B. 7.5×10﹣4 C. 7.5×10﹣5 D. 75×10﹣6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com