
【题目】如图,正方形ABCD的边长是2,∠DAC的平分线交DC于点E,若点P、Q分别是AD和AE上的动点,则DQ+PQ的最小值为 .

【答案】![]() .
.
【解析】
试题过D作AE的垂线交AE于F,交AC于D′,再过D′作D′P′⊥AD,由角平分线的性质可得出D′是D关于AE的对称点,进而可知D′P′即为DQ+PQ的最小值.
作D关于AE的对称点D′,再过D′作D′P′⊥AD于P′,

∵DD′⊥AE,
∴∠AFD=∠AFD′,
∵AF=AF,∠DAE=∠CAE,
∴△DAF≌△D′AF,
∴D′是D关于AE的对称点,AD′=AD=2,
∴D′P′即为DQ+PQ的最小值,
∵四边形ABCD是正方形,
∴∠DAD′=45°,
∴AP′=P′D′,
∴在Rt△AP′D′中,
P′D′2+AP′2=AD′2,AD′2=4,
∵AP′=P′D',
2P′D′2=AD′2,即2P′D′2=4,
∴P′D′=![]()
,即DQ+PQ的最小值为![]() .
.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
【题目】无人机技术我国逐渐发展迅速,全球首款吨位级货运无人机从设计到总装在四川成都双流区完成,现有两架航拍无人机:1号无人机从海拔5米处出发,以1米/秒的速度上升。与此同时,2号无人机从海拔15米处出发,以0.5米/秒的速度上升(设无人机上升时间为![]() 秒)。
秒)。
(1)求出1号无人机所在位置的海拔![]() (米)与
(米)与![]() 之间的关系式和2号无人机所在位置的海拔
之间的关系式和2号无人机所在位置的海拔![]() (米)与
(米)与![]() 之间的关系式?
之间的关系式?
(2)在某一时刻两架无人机能否位于同一高度?如果能,请求出无人机上升的时间与高度?如果不能,请说明理由.
(3)上升多少时间,两架无人机所在位置的海拔相差5米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解八年级学生对![]() (科学)、
(科学)、![]() (技术)、
(技术)、![]() (工程)、
(工程)、![]() (艺术)、
(艺术)、![]() (数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:
(数学)中哪一个领域最感兴趣的情况,该校对八年级学生进行了抽样调查,根据调查结果绘制成如下的条形图和扇形图,请根据图中提供的信息,解答下列问题:

(1)这次抽样调查共调查了多少名学生?
(2)补全条形统计图;
(3)求扇形统计图中![]() (数学)所对应的圆心角度数;
(数学)所对应的圆心角度数;
(4)若该校八年级学生共有400人,请根据样本数据估计该校八年级学生中对![]() (科学)最感兴趣的学生大约有多少人?
(科学)最感兴趣的学生大约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
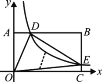
【题目】如图,在以O为原点的直角坐标系中,矩形OABC的两边OC、OA分别在x轴、y轴的正半轴上,反比例函数![]() (x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
(x>0)与AB相交于点D,与BC相交于点E,若BD=3AD,且△ODE的面积是9,则k的值是( )
A.![]() B.
B.![]() C.
C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B![]() 90°,AB
90°,AB![]() 4,BC
4,BC![]() 2,以AC为边作△ACE,∠ACE
2,以AC为边作△ACE,∠ACE![]() 90°,AC=CE,延长BC至点D,使CD
90°,AC=CE,延长BC至点D,使CD![]() 5,连接DE.求证:△ABC∽△CED.
5,连接DE.求证:△ABC∽△CED.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)该二次函数图象的对称轴是x![]() ;
;
(2)若该二次函数的图象开口向下,当![]() 时,
时, ![]() 的最大值是2,求当
的最大值是2,求当![]() 时,
时, ![]() 的最小值;
的最小值;
(3)若对于该抛物线上的两点![]() ,
, ![]() ,当
,当![]() ,
, ![]() 时,均满足
时,均满足![]() ,请结合图象,直接写出
,请结合图象,直接写出![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图AO和BD相交于点O,E是CD上一点,F是OD上一点,EF∥OC,∠1=∠A
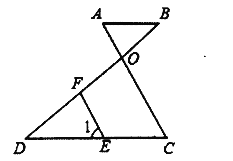
(1)试判断AB和CD的位置关系,并说明理由;
(2)若∠B=50°,∠1=65°,求∠DOC的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com