
分析 (1)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a的值代入计算即可求出值.
解答 解:(1)原式=$\frac{a+1}{a-1}$•(a+1)(a-1)=(a+1)2,
当a=$\sqrt{2}$-1时,原式=2;
(2)原式=$\frac{{a}^{2}-1-4a+5}{a-1}$÷$\frac{a-2}{a(a-1)}$=$\frac{(a-2)^{2}}{a-1}$•$\frac{a(a-1)}{a-2}$=a(a-2),
当a=-1时,原式=3.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


科目:初中数学 来源: 题型:解答题
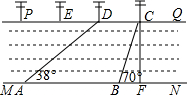 如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).
如图,河流的两岸MN、PQ互相平行,河岸PQ上有一排间隔为50m的电线杆C、D、E…某人在河岸MN的A处测得∠DAN=38°,然后沿河岸走了120米到达B处,测得∠CBN=70°.求河流的宽度CF(结果精确到0.1,参考数据sin38°≈0.62,cos38°≈0.79,tan38°≈0.78,Sin70°≈0.94,cos70°≈0.34,tan70°≈2.75).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 干家务活平均时间 | 频数 | 百分比 |
| A | 10 | 25% |
| B | a | 62.5% |
| C | 5 | b |
| 合计 | c | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com