
| A. | y1>y2 | B. | y1<y2 | C. | .y1≥y2 | D. | y1≤y2 |
分析 先求出抛物线的对称轴,确定抛物线的开口方向,再求出点(x1,y1)的对称点(10-x1,y1),根据二次函数的性质即可得出结果.
解答 解:∵抛物线y=ax2+bx+c交x轴于(3,0)(7,0),
∴对称轴为:x=$\frac{3+7}{2}$=5,
即x=5,
∵当x=5时,y<0,
∴抛物线的开口向上,
即a>0;
∴当x<5时,y随x的增大而减小;
当x>5时,y随x的增大而增大;
∵点(x1,y1)的对称点为:(10-x1,y1),
而5<10-x1<6,
∴点(x2,y2)在点(10-x1,y1)的上方,
∴y1<y2;
故选:B.
点评 本题考查了抛物线与x轴的交点的性质、对称轴的求法、开口方向、二次函数的性质;熟练掌握抛物线与x轴的交点性质、二次函数的性质是解决问题的关键.


科目:初中数学 来源: 题型:选择题
| A. | 不变 | B. | 扩大为原来的5倍 | ||
| C. | 扩大为原来的10倍 | D. | 缩小为原来的$\frac{1}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 16 | B. | 17 | C. | 18 | D. | 19 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (一)问题背景:小明是爱学习的人,通过网络搜索到有5种求三角形面积公式的方法.
(一)问题背景:小明是爱学习的人,通过网络搜索到有5种求三角形面积公式的方法.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
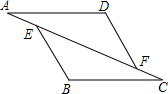 如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?
如图,已知:在△AFD和△CEB中,点A,E,F,C在同一条直线上,AE=CF,∠B=∠D,AD∥BC,请问:AD与BC相等吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 4$\sqrt{2}$ | B. | 5$\sqrt{2}$ | C. | 2$\sqrt{2}$ | D. | 3$\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com