
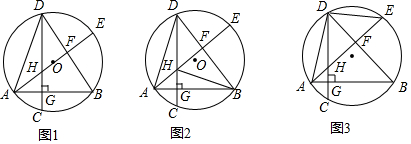
分析 (1)如图1中,连接BE,由DG∥BE,推出∠AEB=∠AHG,由∠ADB=∠AEB,即可推出∠ADB=∠AHG.
(2)连接AC、DE,EB、AC、BC.只要证明HG=CG,∠EDB=∠CDB,根据等腰三角形三线合一即可证明.
(3)过点O作ON⊥DE,OM⊥AB垂足分别为N、M,连接OD、OE、OA、OB.只要证明△NOE≌△MBO,推出NE=OM=3,OB=$\sqrt{{3}^{3}+{4}^{2}}$=5,在RT△OMB中,根据sin∠OBM=$\frac{OM}{OB}$,计算即可.
解答 证明:(1)如图1中,连接BE,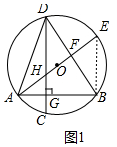
∵AE是⊙O的直径∴∠ABE=90°,
∵DG⊥AB,
∴∠ABE=∠AGD=90°,
∴DG∥BE,
∴∠AEB=∠AHG,
∵∠ADB=∠AEB
∴∠ADB=∠AHG.
(2)连接AC、DE,EB、AC、BC.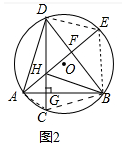
∠GBC=∠HBG,DG⊥AB
∴∠GHB=∠BCH,BH=BC,
∴HG=CG,
∴AH=AC,∠AHC=∠HCA,∠BAC=∠HAG
∵∠AED=∠ACH,∠DHE=∠AHC,
∴∠AED=∠DHE,
∴DH=DE,
∵∠EDB=∠EAB,∠CDB=∠BAC,
∴∠EDB=∠CDB,
∴HF=EF.
(3)过点O作ON⊥DE,OM⊥AB垂足分别为N、M,连接OD、OE、OA、OB.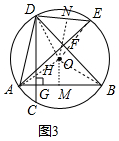
∴BM=$\frac{1}{2}$AB=4,
∵DH=DE=6,HF=EF,
∴DF⊥AE,
∴∠DAE+∠BDA=90°,
∵∠E O D=2∠DAE∠AO B=2∠ADB,
∴∠BOA+∠EOD=180°,
∵∠DOE=2∠NOE∠AOB=2∠BOM,
∴∠NOE+∠BOM=90°∠NOE+∠NEO=90°,
∵∠NEO=∠BOM,OE=OB,
∴△NOE≌△MBO
∴NE=OM=3,
∴OB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵∠ADB=∠BOM,
∴∠DAF=∠OBM,
在RT△OMB中sin∠OBM=$\frac{OM}{OB}$=$\frac{3}{5}$
∴sin∠DAE=$\frac{3}{5}$.
点评 本题考查圆综合题、同弧所对的圆周角相等、垂径定理、勾股定理、全等三角形的判定和性质、锐角三角函数等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:解答题
| 一户居民一个月用电量的范围 | 电费价格(单位:元/度) |
| 不超过150度 | a |
| 超过150度但不超过300度的部分 | 0.65 |
| 超过300度的部分 | 0.9 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )
一辆货车从A地开往B地,一辆小汽车从B地开往A地.同时出发,都匀速行驶,各自到达终点后停止.设货车、小汽车之间的距离为s(千米),货车行驶的时间为t(小时),S与t之间的函数关系如图所示.下列说法中正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
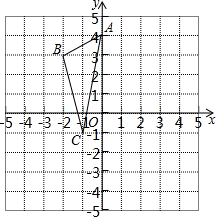 如图,网格中每个小正方形的边长均为1,已知三角形ABC及三角形外一点D,平移三角形ABC使点A(0,4)移动到点D(3,2),得到三角形DEF,B(-2,3)的对应点为E,C(-1,-1)对应点F.
如图,网格中每个小正方形的边长均为1,已知三角形ABC及三角形外一点D,平移三角形ABC使点A(0,4)移动到点D(3,2),得到三角形DEF,B(-2,3)的对应点为E,C(-1,-1)对应点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
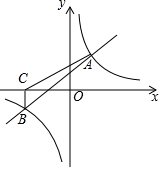 如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.
如图,一次函数y=x+2与反比例函数y=$\frac{k}{x}$的图象相交于A(2,m),B(-4,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
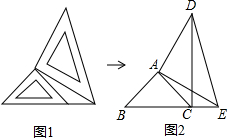 如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).
如图,两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.请找出图2中的全等三角形,并给予证明(不再添加其它线段,不再标注或使用其它字母).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com