
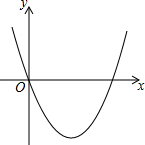
 如图,这个二次函数图象的表达式可能是y=x2-x.(只写出一个)
如图,这个二次函数图象的表达式可能是y=x2-x.(只写出一个) 分析 根据二次函数的图象开口向上知道a>0,又对称轴x=-$\frac{b}{2a}$>0,得出b<0,二次函数的图象过原点,可以得到c=0,所以解析式满足a>0,b<0,c=0即可.
解答 解:∵二次函数的图象开口向上,
∴a>0,
∵对称轴x=-$\frac{b}{2a}$>0,
∴b<0,
∵二次函数的图象过原点,
∴c=0.
故解析式满足a>0,b<0,c=0即可,
如y=x2-x;
故答案为:y=x2-x.
点评 此题是开放性试题,考查函数图形及性质的综合运用,对考查学生所学函数的深入理解、掌握程度具有积极的意义,但此题若想答对需要满足所有条件,如果学生没有注意某一个条件就容易错.本题的结论是不唯一的,其解答思路渗透了数形结合的数学思想.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
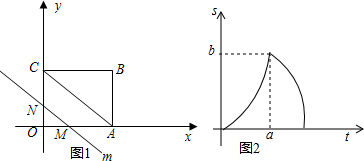
 如图,抛物线y=-x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.
如图,抛物线y=-x2+6x交x轴正半轴于点A,顶点为M,对称轴MB交x轴于点B.过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
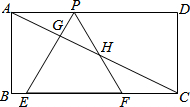 如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.
如图,已知矩形ABCD,AB=$\sqrt{3}$,BC=3,在BC上取两点E,F(E在F左边),以EF为边作等边三角形PEF,使顶点P在AD上,PE,PF分别交AC于点G,H.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
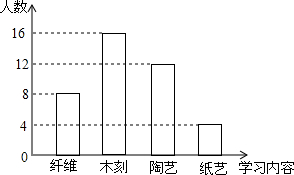 某校初二学年学生即将参加劳动实践基地的学习活动,为了解学生对学习内容的喜爱情况,学校决定围绕“纸艺、木刻、陶艺、纤维四项学习内容中,你参加哪一项(每人必选且只选一项)的问题”,在全学年范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题:
某校初二学年学生即将参加劳动实践基地的学习活动,为了解学生对学习内容的喜爱情况,学校决定围绕“纸艺、木刻、陶艺、纤维四项学习内容中,你参加哪一项(每人必选且只选一项)的问题”,在全学年范围内随机抽取部分学生进行问卷调查,并将调查结果绘制成如图所示的条形统计图,请根据图中提供的信息解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
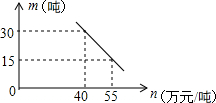 某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:
某工厂生产一种产品,当产量至少为10吨,但不超过55吨时,每吨的成本y(万元)与产量x(吨)之间是一次函数关系,函数y与自变量x的部分对应值如表:| x(吨) | 10 | 20 | 30 |
| y(万元/吨) | 45 | 40 | 35 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com