
| A. | 不等式的两边都加上(或都减去)同一个数或同一个整式,不等号方向不变 | |
| B. | 不等式的两边都乘以(或都除以)同一个正数,不等号的方向不变 | |
| C. | 不等式的两边都乘以(或都除以)同一个负数,不等号的方向改变 | |
| D. | 乘法分配律 |
科目:初中数学 来源: 题型:选择题
| A. | 若a+b=0,则$\frac{a}{b}$=-1 | B. | 若|a|=-a,则a<0 | ||
| C. | 若a>b>0,则-a<-b<0 | D. | 若a<b<0,则$\frac{1}{a}$<$\frac{1}{b}$<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{2}{a}$ | B. | $\frac{a}{2}$ | C. | $\frac{b}{2a}$ | D. | 2a |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 选取50名女生 | B. | 选取50名男生 | ||
| C. | 选取一个班级的学生 | D. | 随机选取50名初一学生 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.
如果抛物线C1的顶点在抛物线C2上,同时,抛物线C2的顶点在抛物线C1上,那么,我们称抛物线C1与C2关联.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
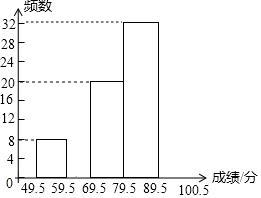 6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:
6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频数分布表和不完整的频数分布直方图如下:| 分组 | 频数 | 所占百分比 |
| 49.5~59.5 | 8 | 8% |
| 59.5~69.5 | 12 | 12% |
| 69.5~79.5 | 20 | 20% |
| 79.5~89.5 | 32 | 32% |
| 89.5~100.5 | 28 | a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com