
分析 (1)直接利用公因式的定义分析得出答案;
(2)直接提取公因式3x,进而分解因式即可;
(3)直接提取公因式ax,进而分解因式即可;
(4)直接提取公因式(x-1),进而分解因式即可;
(5)直接提取公因式4an,进而分解因式即可;
(6)直接提取公因式4(x-y)2,进而分解因式即可.
解答 解:(1)多项式15a3b2-5a2b+20a2b3的各项公因式是:5a2b,
故答案为:5a2b;
(2)3x3+6x=3x(x2+2);
故答案为:3x(x2+2);
(3)3ax2-a2x+10ax=ax(3x-a+10);
故答案为:ax(3x-a+10);
(4)13(x-1)2-2b(x-1)=(x-1)(13x-13-2b);
故答案为:(x-1)(13x-13-2b);
(5)8a2n-4an=4an×(2an-1);
故答案为:(2an-1);
(6)12x(x-y)2-8(x-y)3
=4(x-y)2×[3x-2(x-y)]
=4(x-y)2×(x+2y).
故答案为:(x+2y).
点评 此题主要考查了提取公因式法分解因式,正确找出公因式是解题关键.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在△ABC中,BC=a,AC=b,AB=c;
在△ABC中,BC=a,AC=b,AB=c;查看答案和解析>>
科目:初中数学 来源: 题型:解答题
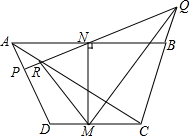 等腰梯形ABCD中,M和N分别为CD、AB的中点.过N作直线PQ和AD和CB的延长线分别交于P和Q,AC和PQ交于点R,求证:∠NMR=∠NMQ.
等腰梯形ABCD中,M和N分别为CD、AB的中点.过N作直线PQ和AD和CB的延长线分别交于P和Q,AC和PQ交于点R,求证:∠NMR=∠NMQ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com