
����Ŀ��ij�̳��ڴ����ڼ�涨���̳���������Ʒ����۵�80%���ۣ�ͬʱ���˿��ڸ��̳�������һ���������·��������Ӧ���Ľ�ȯ��
���ѽ��a��Ԫ����Χ | 200��a��400 | 400��a��500 | 500��a��700 | 700��a��900 | �� |
��ý�ȯ�Ľ����Ԫ�� | 30 | 60 | 100 | 130 | �� |
�������������������˿����̳��ڹ�����Ի��˫���Żݡ����磬������Ϊ450Ԫ����Ʒ�������ѽ��Ϊ![]() Ԫ����õ��Żݶ�Ϊ450����1-80%��+30=120Ԫ���蹺�����Ʒ�õ����Ż���=������Ʒ��õ��Żݶ�����Ʒ�ı�ۡ�
Ԫ����õ��Żݶ�Ϊ450����1-80%��+30=120Ԫ���蹺�����Ʒ�õ����Ż���=������Ʒ��õ��Żݶ�����Ʒ�ı�ۡ�
��1������һ�����Ϊ1000Ԫ����Ʒ���˿͵õ����Ż����Ƕ��٣�
��2�����ڱ����500Ԫ��800Ԫ֮������500Ԫ��800Ԫ������Ʒ���˿�����Ϊ����Ԫ����Ʒ�����Եõ�![]() ���Ż��ʣ�
���Ż��ʣ�
���𰸡���1�� 33%����2��������Ϊ750Ԫ����Ʒ���Եõ�![]() ���Ż�����
���Ż�����
��������
�����������1������һ�����Ϊ1000Ԫ����Ʒ���������и������Żݶ1000����1-80%��+130=330��Ԫ�����Ա�۾����Ż��ʣ�
��2���蹺����ΪxԪ����Ʒ���Եõ�![]() ���Ż��ʣ�������Ϊ500Ԫ��800Ԫ֮�����Ʒʱ�����ѽ��a��400Ԫ��640Ԫ֮����Ȼ��ͷ�������㣬��400��a��500ʱ��500��x��625ʱ���������г����������ע��ⷽ��ʱҪ���ʵ�����������
���Ż��ʣ�������Ϊ500Ԫ��800Ԫ֮�����Ʒʱ�����ѽ��a��400Ԫ��640Ԫ֮����Ȼ��ͷ�������㣬��400��a��500ʱ��500��x��625ʱ���������г����������ע��ⷽ��ʱҪ���ʵ�����������
�����������1���Żݶ1000����1-80%��+130=330��Ԫ��
�Ż��ʣ�![]() ��100%=33%��
��100%=33%��
��2���蹺����ΪxԪ����Ʒ���Եõ�![]() ���Ż�����������Ϊ500Ԫ��800Ԫ֮�����Ʒʱ�����ѽ��a��400Ԫ��640Ԫ֮����
���Ż�����������Ϊ500Ԫ��800Ԫ֮�����Ʒʱ�����ѽ��a��400Ԫ��640Ԫ֮����
����400��a��500ʱ��500��x��625
�����⣬�ã�0��2x+60=![]() x
x
��ã�x=450
��450��500���������⣬����ȥ��
����500��a��640ʱ��625��x��800
�����⣬�ã�0��2x+100=![]() x
x
��ã�x=750
��625��750��800������������
�𣺹�����Ϊ750Ԫ����Ʒ���Եõ�![]() ���Ż�����
���Ż�����


 ����С��ʿ���������ϵ�д�
����С��ʿ���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�ǵȱ���ABC��һ�㣬��AOB=110����BOC=![]() ,����BOC�Ƶ�C��˳ʱ�뷽����ת60����ADC������OD
,����BOC�Ƶ�C��˳ʱ�뷽����ת60����ADC������OD
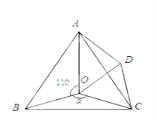
��1����COD��ʲô�����Σ�˵�����ɣ�
��2����AO=![]() ��AD=
��AD=![]() ,OD=
,OD=![]() ��
��![]() ����1������������
Ϊ����1������������![]() �Ķ���
�Ķ���
��3����![]() Ϊ���ٶ�ʱ����AOD�ǵ��������Σ�
Ϊ���ٶ�ʱ����AOD�ǵ��������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC �У�BD��CE�ֱ���AC��AB�ϵĸߣ�BD��CE���ڵ�O��BE=CD��
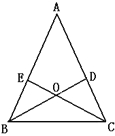
��1����ABC�ǵ�����������Ϊʲô��
��2����O����A��ƽ��������Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() �У�AB= 20cm��BC=16cm����DΪ�߶�AB���е㣬����P��2cm/s���ٶȴ�B�����������BC���˶���ͬʱ��Q��a cm/s��a��0��a��2�����ٶȴ�C��������߶�CA���˶������˶�ʱ��Ϊx����
�У�AB= 20cm��BC=16cm����DΪ�߶�AB���е㣬����P��2cm/s���ٶȴ�B�����������BC���˶���ͬʱ��Q��a cm/s��a��0��a��2�����ٶȴ�C��������߶�CA���˶������˶�ʱ��Ϊx����
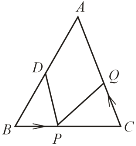
��1����AB=AC��P���߶�BC�ϣ���aΪ��ֵʱ���ܹ�ʹ��BPD����CQPȫ�ȣ�
��2����![]() ������������
������������![]() Ϊֱ�������Σ�
Ϊֱ�������Σ�
��3����![]() ����
����![]() �Ķ���Ϊ����ʱ��
�Ķ���Ϊ����ʱ��![]() Ϊ���������Σ�����ֱ��д���𰸣�����д����������
Ϊ���������Σ�����ֱ��д���𰸣�����д����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
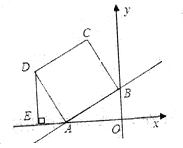
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=0.5x+2��x�ᡢy��ֱ���A��B���㣬��ABΪ���ڵڶ���������������ABCD������D��DE��x�ᣬ����ΪE.
(1)���A��B�����꣬�����AB�ij���
(2)���D�����ꣻ
(3)���ܷ���x������һ��M��ʹ��MDB���ܳ���С������ܣ������M������ꣻ������ܣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ���������Ĺ�������������������壬�������ˣ������ʰ�����Ҫʲô���ͣ������¶Թ���˵������ֻҪ�������ϵ�һ���һ���ף��ڶ���Ŷ���������������������ĸ��ʮ����������������������������̾��С���������ΪҪ���˶�����ʳ������ڴ�Ӧ��,�������������
��1������֪��,�������干��64������,���ڵ�64����Ӧ�Ŷ����ף������ݱ�ʾ��
��2����̽������1���е�����ĩλ�����Ƕ���?����Ҫд��̽����������
��3����֪����������˰����¶���������?Ϊ����������,��������������Ľ��������
�÷�����ʾ����ѭ��С����![]() ��
��
������![]() ������ʽ����ͬʱ����10,��
������ʽ����ͬʱ����10,��![]() ����
����
����![]() ������
������![]() ,��
,��![]() ����
����![]() ��
��
��������Ͻⷨ���������������µ������������ݵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���ż���С���A�س������ڶ�����Ĺ�·�ϼ�����·������涨����ʻΪ����������ʻΪ����һ�����ߴ���ʻ��¼���¡�����λ��km��
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | ���ߴ� |
��3 | ��7 | ��9 | ��8 | ��6 | ��5 | ��4 |
��1�����չ�ʱ��A�ض�Զ��
��2���ڵڼ��μ�¼ʱ��A����Զ��
��3����ÿkm����0��2�����ʹ����Ͷ�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ȼ�������ֵ��
��֪����ʽA=3a2��6ab+b2��B=��2a2+3ab��5b2����a=1��b=��1ʱ������A+2B��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���������߳��ֱ�Ϊ2��x��13�����������ε��ܳ�Ϊ�����������������������θ���Ϊ�� ��
A��2�� B��3�� C��13�� D��������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com