
【题目】解方程
(1)6x2﹣x﹣12=0(用配方法)
(2)(x+4)2=5(x+4)
 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:
【题目】已知:图1、图2是两张形状、大小完全相同的网格,网格中的每个小正方形的边长均为![]() .格中各有一个完全相同的三角形,请在图1、图2分别面一条直线,满足以下要求
.格中各有一个完全相同的三角形,请在图1、图2分别面一条直线,满足以下要求

(1)直线与三角形的交点要经过网格的格点(每个小正方形的顶点均为格点)
(2)在图1、图2中分别用不同的方法将三角形分成两个图形其中一个是三角形另一个是四边形,分割后的三角形的面积记为![]() ,四边形的面积为
,四边形的面积为![]() ,且
,且![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
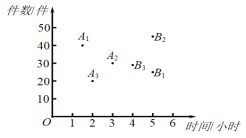
【题目】三名快递员某天的工作情况如图所示,其中点![]() ,
,![]() ,
,![]() 的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点
的横、纵坐标分别表示甲、乙、丙三名快递员上午派送快递所用的时间和件数;点![]() ,
,![]() ,
,![]() ,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
,的横、纵坐标分别表示甲、乙、丙三名快递员下午派送快递所用的时间和件数.有如下三个结论:①上午派送快递所用时间最短的是甲;②下午派送快递件数最多的是丙;③在这一天中派送快递总件数最多的是乙.上述结论中,所有正确结论的序号是( )
A. ①②B. ①③C. ②D. ②③
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=1,点P是BC边上的任意一点(异于端点B、C),连接AP,过B、D两点作BE⊥AP于点E,DF⊥AP于点F.
(1)求证:EF=DF﹣BE;
(2)若△ADF的周长为![]() ,求EF的长.
,求EF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线经过点A(0,4),B(1,0),C(5,0),其对称轴与x轴相交于点M.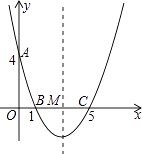
(1)求抛物线的解析式和对称轴;
(2)在抛物线的对称轴上是否存在一点P,使△PAB的周长最小?若存在,请求出点P的坐标;若不存在,请说明理由;
(3)连接AC,在直线AC的下方的抛物线上,是否存在一点N,使△NAC的面积最大?若存在,请求出点N的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O的半径为2,A为⊙O外一点,过点A作⊙O的一条切线AB,切点是B,AO的延长线交⊙O于点C,若∠BAC=30°,则劣弧 ![]() 的长为 .
的长为 . 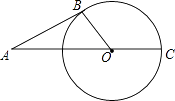
查看答案和解析>>
科目:初中数学 来源: 题型:
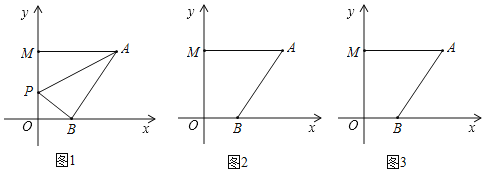
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】荣荣是个爱动脑筋的同学,在发现教材中的用方框在月历中移动的规律后,突发奇想,将连续的偶数2、4、6、8,…排成如下表,并用一个十字形框架住其中的五个数,请你仔细观察十字形框架中数字的规律,并回答下列问题:
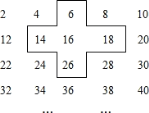
![]() 十字框中的五个数的和与中间的数16有什么关系?
十字框中的五个数的和与中间的数16有什么关系?
![]() 设中间的数为x,用代数式表示十字框中的五个数的和;
设中间的数为x,用代数式表示十字框中的五个数的和;
(3)若将十字框上下左右移动,可框住另外的五个数,其中五个数的和能等于2018吗?如能,写出这五个数,如不能,说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com