
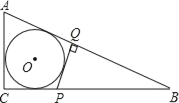
【题目】如图,⊙O内切于Rt△ABC,点P、点Q分别在直角边BC、斜边AB上,PQ⊥AB,且PQ与⊙O相切,若AC=2PQ,则tan∠B的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】
设⊙O的半径是R,PE=PF=x,BQ=y,连接OD,OG,OF,OE,得出正方形CDOE和OGQF,推出OD=CD=CE=OE=GQ=QF=R,求出y=2R,x=![]() R,根据锐角三角函数值求出即可.
R,根据锐角三角函数值求出即可.
解:
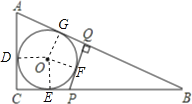
设⊙O的半径是R,PE=PF=x,BQ=y,
连接OD,OG,OF,OE,
∵⊙O内切于Rt△ABC,
∴∠ODC=∠OEC=90°=∠C,AD=AG,
∵OD=OE,
∴四边形CDOE是正方形,
∴OD=CD=CE=OE=R,
同理OG=GQ=FQ=OF=R,
则PQ=CP,AC=AQ,
∵PQ⊥AB,∠C=90°,
∴∠C=∠PQB=90°,
∵∠B=∠B,
∴△BQP∽△BCA,
![]()
根据BG=BE得:y+R=2y-R,
解得:y=2R,
在Rt△PQB中,由勾股定理得:PQ2+BQ2=BP2,
即(2R)2+(R+x)2=(4R-R-x)2,
解得:![]() ,
,
即PQ=![]() ,BQ=2R.
,BQ=2R.
tanB=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
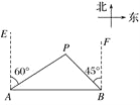
【题目】在我市十个全覆盖工作的推动下,某乡镇准备在相距3千米的A、B两个工厂间修一条笔直的公路,在工厂A北偏东60°方向、工厂北偏西45°方向有一点P,以P点为圆心,1.2千米为半径的区域是一个村庄,问修筑公路时,这个村庄是否有居民需要搬迁?(参考数据:![]() ≈1.4,
≈1.4,![]() ≈1.7)
≈1.7)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于反比例函数y=![]() (k≠0),下列所给的四个结论中,正确的是( )
(k≠0),下列所给的四个结论中,正确的是( )
A. 若点(2,4)在其图象上,则(﹣2,4)也在其图象上
B. 当k>0时,y随x的增大而减小
C. 过图象上任一点P作x轴、y轴的垂线,垂足分别A、B,则矩形OAPB的面积为k
D. 反比例函数的图象关于直线y=x和y=﹣x成轴对称
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 先向右平移2个单位,再向下平移2个单位,得到抛物线
先向右平移2个单位,再向下平移2个单位,得到抛物线![]() .
.

(1)求抛物线![]() 的解析式(化为一般式);
的解析式(化为一般式);
(2)直接写出抛物线![]() 的对称轴与两段抛物线弧围成的阴影部分的面积.
的对称轴与两段抛物线弧围成的阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在铅直高度为200 m的小山上建有一座电视转播塔,某数学兴趣小组为测量电视转播塔的高度,在山脚的点C处测得山顶B的仰角为30°(即∠BCD=300),测得塔顶A的仰角为45°(即∠ACD=45°),请根据以上数据求塔高AB(精确到1 m)(备用数据:![]() ≈1.414,
≈1.414,![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的切线,
的切线,![]() 为切点,直线
为切点,直线![]() 交
交![]() 于点
于点![]() 、
、![]() ,过点
,过点![]() 作
作![]() 的垂线
的垂线![]() ,垂足为点
,垂足为点![]() ,交
,交![]() 于点
于点![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连接
,连接![]() ,
,![]() .
.
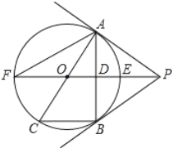
(1)求证:直线![]() 为
为![]() 的切线;
的切线;
(2)试探究线段![]() 、
、![]() 、
、![]() 之间的等量关系,并加以证明;
之间的等量关系,并加以证明;
(3)若![]() ,
,![]() ,求
,求![]() 的值和线段
的值和线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
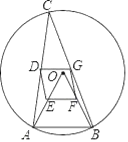
【题目】如图,△ABC是半径为2的⊙O的内接三角形,连接OA、OB,点D、E、F、G分别是CA、OA、OB、CB的中点.
(1)试判断四边形DEFG的形状,并说明理由;
(2)填空:
①若AB=3,当CA=CB时,四边形DEFG的面积是 ;
②若AB=2,当∠CAB的度数为 时,四边形DEFG是正方形.
查看答案和解析>>
科目:初中数学 来源: 题型:
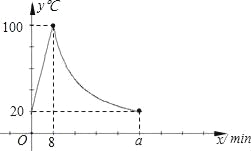
【题目】某小学为每个班级配备了一种可以加热的饮水机,该饮水机的工作程序是:放满水后,接通电源,则自动开始加热,每分钟水温上升10℃,待加热到100℃,饮水机自动停止加热,水温开始下降,水温y(℃)和通电时间x(min)成反比例关系,直至水温降至室温,饮水机再次自动加热,重复上述过程.设某天水温和室温为20℃,接通电源后,水温和时间的关系如下图所示,回答下列问题:
(1)分别求出当0≤x≤8和8<x≤a时,y和x之间的关系式;
(2)求出图中a的值;
(3)下表是该小学的作息时间,若同学们希望在上午第一节下课8:20时能喝到不超过40℃的开水,已知第一节下课前无人接水,请直接写出生活委员应该在什么时间或时间段接通饮水机电源.(不可以用上课时间接通饮水机电源)
时间 | 节次 | |
上 午 | 7:20 | 到校 |
7:45~8:20 | 第一节 | |
8:30~9:05 | 第二节 | |
… | … | |
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某社区为了进一步提高居民珍惜谁、保护水和水忧患意识,提倡节约用水,从本社区5000户家庭中随机抽取100户,调查他们家庭每季度的平均用水量,并将调查的结果绘制成如下的两幅不完整的统计图和表:请根据上面的统计图表,解答下列问题:
(1)在频数分布表中:m= ,n= ;
(2)根据题中数据补全频数直方图;
(3)如果自来水公司将基本季度水量定为每户每季度9吨,不超过基本季度用水量的部分享受基本价格,超出基本季度用水量的部分实行加价收费,那么该社区用户中约有多少户家庭能够全部享受基本价格?
用户季度用水量频数分布表
平均用水量(吨) | 频数 | 频率 |
3<x≤6 | 10 | 0.1 |
6<x≤9 | m | 0.2 |
9<x≤12 | 36 | 0.36 |
12<x≤15 | 25 | n |
15<x≤18 | 9 | 0.09 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com