
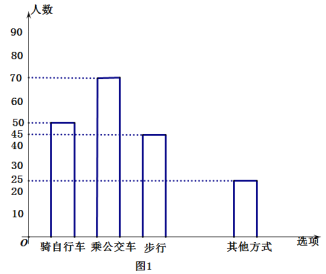
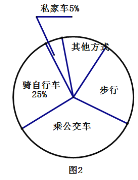
【题目】绿色出行是相对环保的出行方式,通过碳减排和碳中和实现环境资源的可持续利用和交通可持续发展.汽车工业的发展为人类带来了快捷和方便,但同时,汽车的发展也引起了能源的消耗和空气的污染.并且已成为全国各大城市的第一大污染源。实验中学为了解全校学生的交通方式,责成该校七年级(1班)的4位同学对该校部分学生进行了随机调查,按“骑自行车”、“乘公交车”、“步行”、“乘私家车”、“其他方式”设置选项.要求被调查的所有学生从中选一项,并将调查结果绘制成了条形统计图1和扇形统计图2.根据所提供的信息,解答下列问题.
(1)本次调查的人数共有___________人,扇形中步行的圆心角度度数为________.
(2)把条形统计图补充完整.
(3)若该校共有学生3000人,则全校步行的学生大约有多少人数?
(4)根据调查结果对学生的环保出行提一条合理化的建议.
【答案】(1)200人 ,81°;(2)答案见解析;(3)675;(4)学生更多骑行自行车(答案不唯一,有道理即可).
【解析】
(1) 由题意可知骑自行车的百分比和调查人数,故本次调查的人数:![]() ,扇形中步行的圆心角度度数:
,扇形中步行的圆心角度度数:![]() ;
;
(2)由扇形图可知乘私家车比例为5%,且由(1)知调查总人数,故可得乘私家车人数为![]() ,再补全条形图;
,再补全条形图;
(3)先求出步行人数占比,再乘以学校总人数,即可得到答案;
(4)因为题目要求环保,故应该多骑自行车或者多坐公交车.
(1)本次调查的人数:![]() (人),扇形中步行的圆心角度数:
(人),扇形中步行的圆心角度数:![]() =81°;
=81°;
(2)由扇形图可知乘私家车比例为5%,且由(1)知调查总人数,故可得乘私家车人数为![]() =10,再补全条形图如下:
=10,再补全条形图如下:
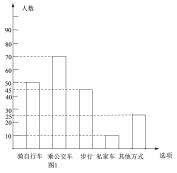
(3)45÷200×3000=675(人)
答:全校3000学生中不行动人数大约为675人
(4)学生更多骑行自行车(答案不唯一,有道理即可).


科目:初中数学 来源: 题型:
【题目】已知∠AOD=160°,OB、OC、OM、ON是∠AOD内的射线.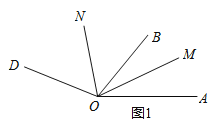
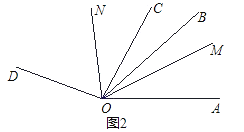
(1)如图1,若OM平分∠AOB,ON平分∠BOD.当OB绕点O在∠AOD内旋转时,求∠MON的大小;
(2)如图2,若∠BOC=20°,OM平分∠AOC,ON平分∠BOD.当∠BOC绕点O在∠AOD内旋转时,求∠MON的大小;
(3)在(2)的条件下,若∠AOB=10°,当∠B0C在∠AOD内绕着点O以2度/秒的速度逆时针旋转t秒时,∠AOM=![]() ∠DON.求t的值.
∠DON.求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小华将一条直角边长为1的一个等腰直角三角形纸片(如图1),沿它的对称轴折叠1次后得到一个等腰直角三角形(如图2),再将图2的等腰直角三角形沿它的对称轴折叠后得到一个等腰直角三角形(如图3),则图3中的等腰直角三角形的一条腰长为_________;同上操作,若小华连续将图1的等腰直角三角形折叠n次后所得到的等腰直角三角形(如图n+1)的一腰长为_________.
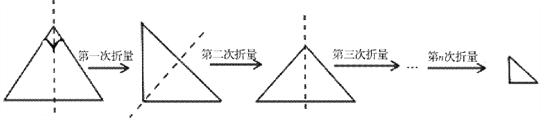
图1 图2 图3 图n+1
查看答案和解析>>
科目:初中数学 来源: 题型:
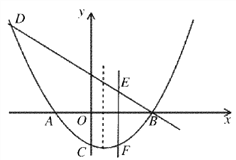
【题目】如图,已知拋物线![]() (k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线
(k为常数,且k>0)与x轴的交点为A、B,与y轴的交点为C,经过点B的直线![]() 与抛物线的另一个交点为D.
与抛物线的另一个交点为D.
(1)若点D的横坐标为x= -4,求这个一次函数与抛物线的解析式;
(2)若直线m平行于该抛物线的对称轴,并且可以在线段AB间左右移动,它与直线BD和抛物线分别交于点E、F,求当m移动到什么位置时,EF的值最大,最大值是多少?
(3)问原抛物线在第一象限是否存在点P,使得△APB∽△ABC?若存在,请求出这时k的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】青岛、大连两个城市各有机床12台和6台,现将这些机床运往海南10台和厦门8台,每台费用如表一:
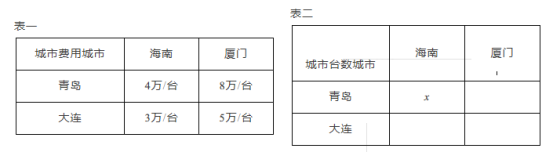
问题1:如表二,假设从青岛运往海南![]() 台机床,并且从青岛、大连运往海南机床共花费36万元,求青岛运往海南机床台数.
台机床,并且从青岛、大连运往海南机床共花费36万元,求青岛运往海南机床台数.
问题2:在问题1的基础上,问从青岛、大连运往海南、厦门的总费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形![]() 在平面直角坐标系中,
在平面直角坐标系中, ![]() ,
,![]() ,把矩形
,把矩形![]() 沿直线
沿直线![]() 对折使点
对折使点![]() 落在点
落在点![]() 处,直线
处,直线![]() 与
与![]() 的交点分别为
的交点分别为![]() ,点
,点![]() 在
在![]() 轴上,点
轴上,点![]() 在坐标平面内,若四边形
在坐标平面内,若四边形![]() 是菱形,则菱形
是菱形,则菱形![]() 的面积是( )
的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽、小明练习打字,已知小丽比小明每分钟多打80个字,小丽打3500个字的时间与小明打2500个字的时间相同.
(1)小丽、小明每分钟分别可打多少字?
(2)如果有一份总字数为m的稿件需要输入电脑,小丽工作了![]() 个小时后余下的输入工作由小明继续完成,则小明还需要工作多少小时?(所得结果用含有
个小时后余下的输入工作由小明继续完成,则小明还需要工作多少小时?(所得结果用含有![]() 的代数式表示;
的代数式表示;![]() 均为大于零的正数)
均为大于零的正数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A、B两地相距480km,C地在A、B两地之间.一辆轿车以100km/h的速度从A地出发匀速行驶,前往B地.同时,一辆货车以80km/h的速度从B地岀发,匀速行驶,前往A地.
(1)当两车相遇时,求轿车行驶的时间;
(2)当两车相距120km时,求轿车行驶的时间;
(3)若轿车到达B地后,立刻以120km/h的速度原路返回,再次经过C地,两次经过C地的时间间隔为2.2h,求C地距离A地路程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用配方法解下列方程,其中应在方程左右两边同时加上4的是( )
A. x2﹣2x=5 B. x2+4x=5 C. 2x2﹣4x=5 D. 4x2+4x=5
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com