
【题目】已知关于x的方程(a﹣1)x2+2x+a+1=0.
(1)若该方程有一根为0,求a的值及方程的另一根;
(2)当a为何值时,方程仅有一个实数根?求出此时a的值.
【答案】(1)a=﹣1,方程的另一根为1.(2)a的值为﹣1或﹣![]() 或
或![]() .
.
【解析】
(1)将x=0代入方程(a﹣1)x2+2x+a+1=0,可求出a的值,再将得到的a值带入原方程,求出另一个方程的解.
(2)分两种情况,当a=1和a≠1的情况,当a=1时,带入求得x的值,当a≠1时,根据b2﹣4ac=0,求出a的值,综合以上两种情况,可解出a的值.
解:(1)将x=0代入方程(a﹣1)x2+2x+a+1=0得a+1=0,
解得:a=﹣1.
将a=﹣1代入原方程得﹣2x2+2x=0,
解得:x1=0,x2=1.
∴a=﹣1,方程的另一根为1.
(2)①当a=1时,方程为2x+2=0,
解得:x=﹣1;
②当a≠1时,由b2﹣4ac=0得4﹣4(a﹣1)(a+1)=0,
解得:a=﹣![]() 或
或![]() .
.
故a的值为﹣1或﹣![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,M、N是对角线AC上的两个动点,P是正方形四边上的任意一点,且AB=4,MN=2,设AM=x,在下列关于△PMN是等腰三角形和对应P点个数的说法中,
①当x=0(即M、A两点重合)时,P点有6个;
②当P点有8个时,x=2![]() ﹣2;
﹣2;
③当△PMN是等边三角形时,P点有4个;
④当0<x<4![]() ﹣2时,P点最多有9个.
﹣2时,P点最多有9个.
其中结论正确的是( )

A. ①② B. ①③ C. ②③ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,函数
中,函数![]() (
(![]() )的图象
)的图象![]() 经过点
经过点![]() (4,1),直线
(4,1),直线![]() 与图象
与图象![]() 交于点
交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)求![]() 的值;
的值;
(2)横、纵坐标都是整数的点叫做整点.记图象![]() 在点
在点![]() ,
,![]() 之间的部分与线段
之间的部分与线段![]() ,
,![]() ,
,![]() 围成的区域(不含边界)为
围成的区域(不含边界)为![]() .
.
①当![]() 时,直接写出区域
时,直接写出区域![]() 内的整点个数;
内的整点个数;
②若区域![]() 内恰有4个整点,结合函数图象,求
内恰有4个整点,结合函数图象,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知⊙O的半径为10,圆心O到弦AB的距离为5,则弦AB所对的圆周角的度数是( )
A. 30° B. 60° C. 30°或150° D. 60°或120°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
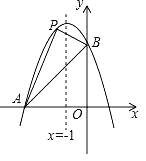
(1)求此抛物线的解析式.
(2)若点Q是对称轴上一动点,当OQ+BQ最小时,求点Q的坐标.
(3)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB面积的最大值,并求出此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
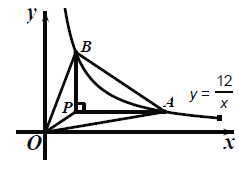
【题目】如图,点![]() 、
、![]() 是函数
是函数![]() 上两点,点
上两点,点![]() 为一动点,作
为一动点,作![]() 轴,
轴,![]() 轴,下列结论:①
轴,下列结论:①![]() ≌
≌![]() ;②
;②![]() ;③若
;③若![]() ,则
,则![]() 平分
平分![]() ;④若
;④若![]() ,则
,则![]() .其中正确的序号是__________(把你认为正确的都填上).
.其中正确的序号是__________(把你认为正确的都填上).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中装有大小和形状相同的3个红球和2个白球,把它们充分搅匀.
(1)“从中任意抽取1个球不是红球就是白球”是 事件,“从中任意抽取1个球是黑球”是 事件;
(2)从中任意抽取1个球恰好是红球的概率是 ;
(3)学校决定在甲、乙两名同学中选取一名作为学生代表发言,制定如下规则:从盒子中任取两个球,若两球同色,则选甲;若两球异色,则选乙.甲、乙两名同学被选中的概率各是多少?你认为这个规则公平吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
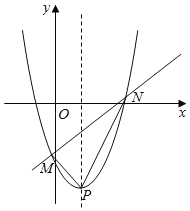
【题目】已知二次函数y=x2+bx+c.
(Ⅰ)若二次函数的图象经过(3,﹣2),且对称轴为x=1,求二次函数的解析式;
(Ⅱ)如图,在(Ⅰ)的条件下,过定点的直线y=﹣kx+k﹣4(k≤0)与(1)中的抛物线交于点M,N,且抛物线的顶点为P,若△PMN的面积等于3,求k的值;
(Ⅲ)当c=b2时,若在自变量x的值满足b≤x≤b+3的情况下,与其对应的函数值y的最小值为21,求此时二次函数的解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com