
分析 (1)先乘方,再乘除,后加减,有括号的先算括号里面的,在同一级运算中要从左到右依次运算;
(2)解分式方程的步骤:①去分母;②求出整式方程的解;③检验;④得出结论.
解答 解:(1)$\sqrt{12}$+|3-$\sqrt{3}$|-2sin60°+(2017-π)0+($\frac{1}{2}$)-2
=2$\sqrt{3}$+3-$\sqrt{3}$-2×$\frac{\sqrt{3}}{2}$+1+$\frac{1}{(\frac{1}{2})^{2}}$
=2$\sqrt{3}$+3-$\sqrt{3}$-$\sqrt{3}$+1+4
=8;
(2)$\frac{2-x}{x-3}$+$\frac{1}{3-x}$=1
整理得$\frac{2-x}{x-3}$-$\frac{1}{x-3}$=1
$\frac{2-x-1}{x-3}=1$
1-x=x-3
解得x=2
经检验:x=2是分式方程的解.
点评 本题主要考查了实数的运算以及解分式方程,解题时注意:实数既可以进行加、减、乘、除、乘方运算,又可以进行开方运算,其中正实数可以开平方.解分式方程时,一定要检验.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{1}{\sqrt{3}}$ | B. | -$\sqrt{3}$ | C. | $\sqrt{3}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
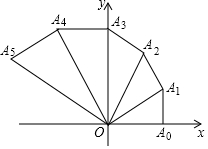 如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为($\frac{\sqrt{3}}{2}$)2016.
如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2016A2017,若点A0(1,0),则点A2017的横坐标为($\frac{\sqrt{3}}{2}$)2016.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com