练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    17．计算：
    （1）$\frac{1}{\sqrt{2}-\sqrt{3}}$+4×$\frac{1}{2\sqrt{2}}$-$\sqrt{（\sqrt{3}-2）^{2}}$
    （2）$\sqrt{（-2）^{2}}$+|1-$\sqrt{2}$|+$\sqrt{3}$-$\frac{1}{\sqrt{3}-\sqrt{2}}$
    （3）$\sqrt{12}$+$\frac{1}{2-\sqrt{3}}$-（2+$\sqrt{3}$）2
    （4）（8-2$\sqrt{15}$）（$\sqrt{5}$+$\sqrt{3}$）2．

    分析 利用二次根式的运算性质即可求出答案．

    解答 解：（1）原式=-$\sqrt{2}$-$\sqrt{3}$+4×$\frac{\sqrt{2}}{4}$-（2-$\sqrt{3}$）=-2；
    （2）原式=2+（$\sqrt{2}$-1）+$\sqrt{3}$-（$\sqrt{3}$+$\sqrt{2}$）=1；
    （3）原式=2$\sqrt{3}$+2+$\sqrt{3}$-（7+4$\sqrt{3}$）=-5-$\sqrt{3}$；
    （4）原式=（8-2$\sqrt{15}$）（8+2$\sqrt{15}$）=64-60=4

    点评 本题考查二次根式的混合运算，涉及二次根式的性质，属于基础题型．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    4．如图，△ABC中，AB=AC，∠BAC=45°，以AB为直径的⊙O交BC于点D，交AC于点E，过B作BF∥DE，交⊙O于点F，过F点作FH∥AC交BC的延长线于点H．
    （1）求证：DE=DC；
    （2）求∠BOF的度数；
    （3）求证：FH与⊙O相切．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

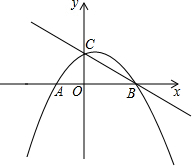    8．如图．在平面直角坐标系中．抛物线y=-$\frac{1}{4}{x}^{2}$+$\frac{1}{2}$x+2与x轴交于A、B两点，与y轴交于点C，点P从B出发．沿射线BA方向以每秒1个单位的速度匀速运动．过点P作PQ⊥x轴．直线PQ分别与直线BC、抛物线交于点Q、K．
    （1）求线段KQ的长度d与点P运动时间t的函数解析式．
    （2）求△CKQ的面积S关于点P运动时间t的函数解析式．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．观察下列等式：
    $\frac{1}{1×2}$=1-$\frac{1}{2}$，$\frac{1}{2×3}$=$\frac{1}{2}$-$\frac{1}{3}$，$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$，
    将以上三个等式两边分别相加得：
    $\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$=1-$\frac{1}{4}$=$\frac{3}{4}$．
    （1）猜想并写出：$\frac{1}{n（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$；
    （2）直接写出下列各式的计算结果：
    ①$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{2011×2012}$=$\frac{2011}{2012}$；
    ②$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{n×（n+1）}$=$\frac{n}{n+1}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．计算下列各题：
    （1）（$\sqrt{2}$+$\sqrt{5}$）（$\sqrt{5}$-$\sqrt{2}$）；
    （2）（-3）0-|-$\sqrt{2}$|+$\sqrt{8}$；
    （3）$\sqrt{24}$×$\sqrt{\frac{1}{3}}$-4$\sqrt{\frac{1}{8}}$×（1-$\sqrt{2}$）0；
    （4）（$\sqrt{18}$+$\frac{1}{5}$$\sqrt{50}$-4$\sqrt{\frac{1}{2}}$）÷$\sqrt{32}$；
    （5）（$\sqrt{{a}^{3}b}$-3ab+$\sqrt{a{b}^{3}}$）÷$\sqrt{a}$•$\frac{1}{\sqrt{b}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．a、b、c、d表示4个有理数，其中每三个数之和是-1，-3，2，17，且a＞b＞c＞d，求a、b、c、d．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．定义：如果M个不同的正整数，对其中的任意两个数，这两个数的积能被这两个数的和整除，则称这组数为M个数的祖冲之数组．如（3，6）为两个数的祖冲之数组，因为（3×6）能被（3+6）整除；又如（15，30，60）为三个数的祖冲之数组，因为（15×30）能被（15+30）整除，（15×60）能被（15+60）整除，（30×60）能被（30+60）整除…
    （1）我们发现，3和6，4和12，5和20，6和30…，都是两个数的祖冲之数组；由此猜测n和n（n-1）（n≥2，n为整数）组成的数组是两个数的祖冲之数组，请证明这一猜想．
    （2）若（3a，4a，5a）是三个数的祖冲之数组，求满足条件的所有三位正整数a．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．观察下列等式：
    22-12=3=（2+1）（2-1），
    32-22=5=（3+2）（3-2），
    42-32=7=（4+3）（4-3），
    试计算：19512-19502+19532-19522+…+20142-20132．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．设x1、x2是一元二次方程x2+5x-2013=0的两个实数根，则x1（x22+4x2-2013）的值为2013．

    查看答案和解析>>

    同步练习册答案