
【题目】如图,直线l上有三个正方形a,b,c,若a,c的面积分别为5和11,则b的面积为( )

A. 16 B. 6 C. 55 D. 26
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y =-x+7与正比例函数y=![]() x的图象交于点A,且与x轴交于点B.
x的图象交于点A,且与x轴交于点B.
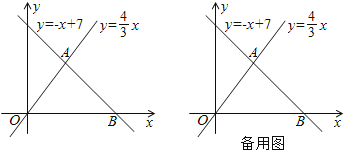
(1)求点A和点B的坐标;
(2)过点A作AC⊥y轴于点C,过点B作直线l∥y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒.
①当t为何值时,以A、P、R为顶点的三角形的面积为8?
②是否存在以A、P、Q为顶点的三角形是直角三角形?若存在,求t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:m,x,y满足:(1)![]() ;(2)﹣2a2by+1与7b3a2是同类项.
;(2)﹣2a2by+1与7b3a2是同类项.
求代数式:2x2﹣6y2+m(xy﹣9y2)﹣(3x2﹣3xy+7y2)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c的图象如图所示,那么一次函数y=bx+c和反比例函数y=![]() 在同一平面直角坐标系中的图象大致是( )
在同一平面直角坐标系中的图象大致是( )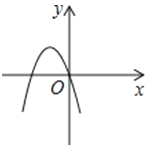
A.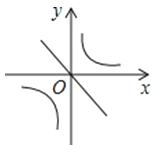
B.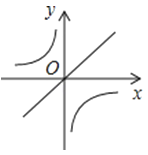
C.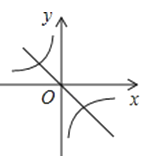
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边![]() 在数轴上的位置如图所示,点A、C对应的数分别为0和
在数轴上的位置如图所示,点A、C对应的数分别为0和![]() ,若
,若![]() 绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2012次后,点B( )
绕顶点沿顺时针方向在数轴上连续翻转,翻转1次后,点B所对应的数为1,则连续翻转2012次后,点B( )

A. 不对应任何数 B. 对应的数是2010
C. 对应的数是2011 D. 对应的数是2012
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】尊师重教是我国的传统美德.教师节当天,出租车司机小王在东西向的街道上免费接送教师,规定向东为正,向西为负,当天出租车的行程如下(单位:千米):
![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() 将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
将最后一名老师送到目的地时,小王距出发地多少千米?方位如何?
![]() 若汽车耗油量为
若汽车耗油量为![]() 升/千米,则当天耗油多少升?
升/千米,则当天耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
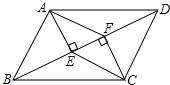
【题目】如图,在□ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F,试判断:
(1)△ABE和△CDF全等吗?请说明理由;
(2)四边形AECF是不是平行四边形,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+3(a≠0)经过A(3,0),B(4,1)两点,且与y轴交于点C.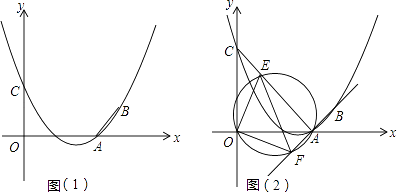
(1)求抛物线y=ax2+bx+3(a≠0)的函数关系式及点C的坐标;
(2)如图(1),连接AB,在题(1)中的抛物线上是否存在点P,使△PAB是以AB为直角边的直角三角形?若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(2),连接AC,E为线段AC上任意一点(不与A、C重合)经过A、E、O三点的圆交直线AB于点F,当△OEF的面积取得最小值时,求点E的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com