
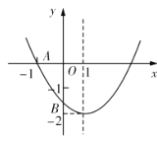
【题目】如图,已知二次函数![]()
![]() 的图像与
的图像与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴的交点
轴的交点![]() 在
在![]() 和
和![]() 之间(不包括这两点),对称轴为直线
之间(不包括这两点),对称轴为直线![]() .下列结论:
.下列结论:
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() .
.
其中正确结论有 __________.
【答案】①③④
【解析】
由①由抛物线的开口方向、对称轴以及与y轴的交点,可得出a>0、b<0、c<0,进而可得出abc>0,结论①正确;②由抛物线的对称轴及点A的坐标,可得出抛物线与x轴的另一交点坐标,结合抛物线的开口可得出当x=4时,![]() >0,结论②错误;③由a>0、b<0、c<0,可得出4acb2<0<8a,结论③正确;④由当x=1时y=ab+c=0,结合b=2a可得出3a=c,再根据2<c<1,即可求出
>0,结论②错误;③由a>0、b<0、c<0,可得出4acb2<0<8a,结论③正确;④由当x=1时y=ab+c=0,结合b=2a可得出3a=c,再根据2<c<1,即可求出![]() ,结论④正确;⑤由ab+c=0、a>0,可得出b+c<0,即b>c,结论⑤错误.综上即可得出结论.
,结论④正确;⑤由ab+c=0、a>0,可得出b+c<0,即b>c,结论⑤错误.综上即可得出结论.
①∵抛物线开口向上,对称轴为直线x=1,与y轴的交点在(0,2)和(0,1)之间,
∴a>0,![]() =1,2<c<1,
=1,2<c<1,
∴b<0,abc>0,结论①正确;
②∵抛物线与x轴交于点A(1,0),对称轴为直线x=1,
∴抛物线与x轴的另一交点坐标为(3,0),
∴当x=4时,![]() >0,结论②错误;
>0,结论②错误;
③∵a>0,b<0,c<0,
∴4ac<0,b2>0,
∴4acb2<0<8a,结论③正确;
④当x=1时,y=ab+c=0,
∴ab=c.
∵b=2a,
∴3a=c.
又∵2<c<1,
∴![]() ,结论④正确;
,结论④正确;
⑤∵当x=1时,y=ab+c=0,a>0,
∴b+c<0,
∴b>c,结论⑤错误.
综上所述:正确的结论有①③④.
故答案为:①③④.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣![]() ,0),点E是AC的中点,连接OE交CD于点F.
,0),点E是AC的中点,连接OE交CD于点F.
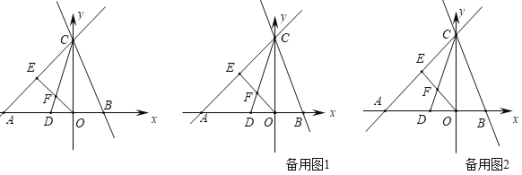
(1)求点F的坐标;
(2)若∠OCB=∠ACD,求k的值;
(3)在(2)的条件下,过点F作x轴的垂线1,点M是直线BC上的动点,点N是x轴上的动点,点P是直线l上的动点,使得以B,P,M、N为顶点的四边形是菱形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC的垂直平分线EF分别交BC,AD于点E,F,若BE=3,AF=5,则AC的长为( )

A. ![]() B.
B. ![]() C. 10D. 8
C. 10D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》中记载:“今有上禾三秉,益实六斗,当下禾十秉.下禾五秉,益实一斗,当上禾二秉.问上、下禾实一秉各几何?”其大意是:今有上等稻子三捆,若打出来的谷子再加六斗,则相当于十捆下等稻子打出来的谷子.有下等稻子五捆,若打出来的谷子再加一斗,则相当于两捆上等稻子打岀来的谷子.问上等、下等稻子每捆能打多少斗谷子?设上等稻子每捆能打x斗谷子,下等稻子每捆能打y斗谷子,根据题意,可列方程组为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=x的图象与反比例函数y=![]() (k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(Ⅰ)当x=4时,求反比例函数y=![]() 的值;
的值;
(Ⅱ)当﹣2<x<﹣1时,求反比例函数y=![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]()
![]() 与
与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于
轴相交于![]() 点,对称轴为
点,对称轴为![]() ,直线
,直线![]() 与抛物线相交于
与抛物线相交于![]() 、
、![]() 两点.
两点.
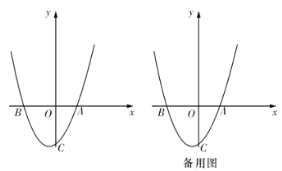
(1)求此抛物线的解析式;
(2)![]() 为抛物线上一动点,且位于
为抛物线上一动点,且位于![]() 的下方,求出
的下方,求出![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标;
的坐标;
(3)设点![]() 在
在![]() 轴上,且满足
轴上,且满足![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
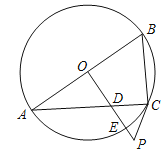
【题目】如图,已知AB是⊙O的直径,过O点作OP⊥AB,交弦AC于点D,交⊙O于点E,且使∠PCA=∠ABC.
(1)求证:PC是⊙O的切线;
(2)若∠P=60°,PC=2,求PE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABO中,∠B=90 ,OB=3,OA=5,以AO上一点P为圆心,PO长为半径的圆恰好与AB相切于点C,则下列结论正确的是( ).
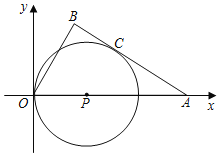
A.⊙P 的半径为![]()
B.经过A,O,B三点的抛物线的函数表达式是![]()
C.点(3,2)在经过A,O,B三点的抛物线上
D.经过A,O,C三点的抛物线的函数表达式是![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com