Question

如图，一次函数y₁＝k₁x＋2与反比例函数y₂＝的图象交于点A (4，m)和B(－8，－2)，与y轴交于点C

1.k₁＝_______，k₂＝______

2.根据函数图象可知，当y₁>y₂时，x的取值范围是______．

3.过点A作AD⊥x轴于点D，点P是反比例函数在第一象限的图象上一点．设直线OP与线段AD交于点E，当S四边形ODAC：S△CE＝3：1时，求点P的坐标

 

Answer 1

 

1.k₁₌ ，k₂=16

2.－8<x<0或x>4  (3)(4，2)

3.P（4√2，2√2）

 解析:(1) 16 (2)－8<x<0或x>4  (3)(4，2)

解：因为一次函数y₁＝k₁x＋2与反比例函数y₂＝的图象交于点A (4，m)和B(－8，－2)

所以联立方程组，则有k₁x＋2=，即k₁x²＋2x= k₂,即k₁x²＋2x- k₂=0

所以，则有4+（-8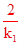）= -，4（-8）=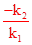

解得：k₁₌ ，k₂=16

（2）由上一问可知，y₁>y₂,即k₁x＋2>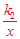

解得

解得：－8<x<0或x>4

解：连接OP，交AD于点E

把B（-8，-2）带入y₁=k₁x+2，得

-2=-8k₁+2

k₁=1/2

∴y₁=1/2x+2

当x=0时，y=2

∴C（0,2）

把点B（-8，-2）带入y₂=k₂/x,得

 k₂=16 ∴y₂=16/x

再把点A（4，m）带入y₂=16/x，得

m=4

∴A（4，4）

S四边形ODAC=1/2X（OC+AD）XOD

=1/2X（2+4)X4

   =12

又∵S四边形ODAC：S△ODE=3：1

   ∴S△ODE=1/2XODXDE=1/2X4XDE=12X1/3，DE=2

   ∴E（4,2）设直线OE的函数解析式为y=kx（k≠0）

∴2=4k， k=1/2∴y=1/2x

∴  y=1/2x，y₂=16/x

解得x=4√2    y=2√2

∴P（4√2，2√2）