
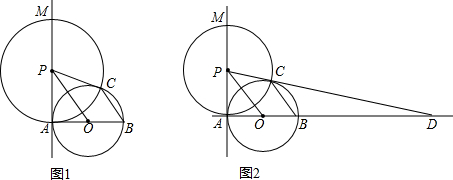
分析 (1)①PC与⊙O相切.易证明△PAO≌△PCO,则∠PAO=∠PCO,由PA是⊙O的切线,可知∠PAO=∠PCO=90°,即可证明结论;
②OP∥BC.由(1)可知∠POA=∠POC,根据同弧所对圆周角是圆心角的一半可知∠ABC=$\frac{1}{2}$∠AOC,根据同位角相等可证明OP∥BC.
(2)根据OP∥BC,可知$\frac{BD}{OD}=\frac{CD}{PD}$,由BD=2AB,可知AD=6OA,OD=5OB,所以PD=5PC,设设PA=PC=R,OA=r,根据勾股定理列方程求出R与r的数量关系,即可在Rt△PAO中求出tan∠ABC=tan∠POA.
解答 (1)①PC与⊙O相切.
证明:如图1,连接OC,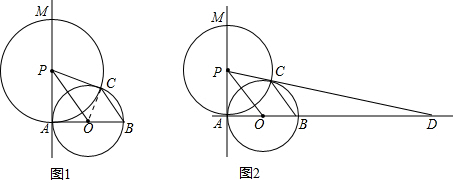 在△PAO和△PCO中,
在△PAO和△PCO中,
$\left\{\begin{array}{l}{OA=OC}\\{PO=PO}\\{PA=PC}\end{array}\right.$,
∴△PAO≌△PCO,
∴∠PAO=∠PCO,
∵PA是⊙O的切线,AB是⊙O的直径,
∴∠PAO=∠PCO=90°,
∴PC与⊙O相切.
②OP∥BC.
证明:∵△PAO≌△PCO,
∴∠POA=∠POC,
又∵∠ABC=$\frac{1}{2}$∠AOC(同弧所对圆周角是圆心角的一半),
∴∠ABC=∠POA,
∴OP∥BC.
(2)解:如图2,
∵BD=2AB,
∴BD=4OB,AD=6OA,
∴$\frac{BD}{OD}=\frac{4}{5}$,
∵OP∥BC,
∴$\frac{BD}{OD}=\frac{CD}{PD}=\frac{4}{5}$,
∴PD=5PC,
设PA=PC=R,OA=r,
∴AD=6r,PD=5R,
∵PA2+AD2=PD2,
∴R2+(6r)2=(5R)2
解得:R=$\frac{\sqrt{6}}{2}$r,
∵tan∠ABC=tan∠POA=$\frac{PA}{OA}$,
∴tan∠ABC═$\frac{PA}{OA}$=$\frac{\frac{\sqrt{6}}{2}r}{r}$=$\frac{\sqrt{6}}{2}$.
点评 本题主要考查了圆的有关性质、切线的性质与判定、平行线分线段成比例定理、勾股定理以及锐角三角函数的综合应用,运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


科目:初中数学 来源: 题型:选择题
| A. | b=-3 | B. | b=-2 | C. | b=-1 | D. | b=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{27}$ | B. | $\sqrt{\frac{1}{5}}$ | C. | $\sqrt{16}$ | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类别 | 频数 | 频率 |
| 助人为乐美德少年 | a | 0.20 |
| 自强自立美德少年 | 3 | b |
| 孝老爱亲美德少年 | 7 | 0.35 |
| 诚实守信美德少年 | 6 | 0.32 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.
某粮油超市平时每天都将一定数量的某些品种的粮食进行包装以便出售,已知每天包装大黄米的质量是包装江米质量的$\frac{5}{4}$倍,且每天包装大黄米和江米的质量之和为45千克.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com