
【题目】随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
(1)“快车”行驶里程不超过5公里计费8元;
(2)“顺风车”行驶里程超过2公里的部分,每公里计费1.2元;
(3)A点的坐标为(6.5,10.4);
(4)从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,其中正确的个数有( )
A.1个
B.2个
C.3个
D.4个
【答案】D
【解析】解:(1)根据“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象可知:
行驶里程不超过5公里计费8元,即(1)正确;
(2)“滴滴顺风车”行驶里程超过2公里的部分,每公里计费为(14.6﹣5)÷(10﹣2)=1.2(元),
故(2)正确;
(3)设x≥5时,“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y1=k1x+b1 ,
将点(5,8)、(10,16)代入函数解析式得:
∴“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y1=1.6x;
当x≥2时,设“滴滴顺风车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y2=k2x+b2 ,
将点(2,5)、(10,14.6)代入函数解析式得: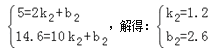
∴“滴滴顺风车”的行驶里程x(公里)与计费y(元)之间的函数关系式为y2=1.2x+2.6.
联立y1、y2得:![]()
∴A点的坐标为(6.5,10.4),(3)正确;
(4)令x=15,y1=1.6×15=24;
令x=15,y2=1.2×15+2.6=20.6.
y1﹣y2=24﹣20.6=3.4(元).
即从哈尔滨西站到会展中心的里程是15公里,则“顺风车”要比“快车”少用3.4元,(4)正确.
综上可知正确的结论个数为4个.
故选D.
(1)根据“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象的拐点为(5,8),即可得知(1)结论成立;(2)根据“单价=超出费用÷超出距离”即可算出)“顺风车”行驶里程超过2公里的部分,每公里计费价格,从而得知(2)成立;(3)设出“滴滴顺风车”与“滴滴快车”超出部分的函数解析式,利用待定系数法求出两个函数解析式,再联立成方程组,解方程组即可得出A点的坐标,从而得知(3)成立;(4)将x=15分别带入y1、y2中,求出费用即可判定(4)成立.综上即可得出结论.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(1)阅读材料:
教材中的问题,如图1,把5个边长为1的小正方形组成的十字形纸板剪开,使剪成的若干块能够拼成一个大正方形,小明的思考:因为剪拼前后的图形面积相等,且5个小正方形的总面积为5,所以拼成的大正方形边长为 ,故沿虚线AB剪开可拼成大正方形的一边,请在图1中用虚线补全剪拼示意图.
(2)类比解决:
如图2,已知边长为2的正三角形纸板ABC,沿中位线DE剪掉△ADE,请把纸板剩下的部分DBCE剪开,使剪成的若干块能够拼成一个新的正三角形.
①拼成的正三角形边长为 ;
②在图2中用虚线画出一种剪拼示意图.
(3)灵活运用:
如图3,把一边长为60cm的正方形彩纸剪开,用剪成的若干块拼成一个轴对称的风筝,其中∠BCD=90°,延长DC、BC分别与AB、AD交于点E、F,点E、F分别为AB、AD的中点,在线段AC和EF处用轻质钢丝做成十字形风筝龙骨,在图3的正方形中画出一种剪拼示意图,并求出相应轻质钢丝的总长度.(说明:题中的拼接都是不重叠无缝隙无剩余)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣1,1),B(﹣3,1),C(﹣1,4).
(1)画出△ABC关于y轴对称的△A1B1C1;
(2)将△ABC绕着点B顺时针旋转90°后得到△A2BC2,请在图中画出△A2BC2,并求出线段BC旋转过程中所扫过的面积(结果保留π).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强公民的节水意识,合理利用水资源,某市采取价格调控手段以达到节水的目的,下表是该市自来水收费价格的价目表.
价目表 | |
每月用水量 | 单价 |
不超出6 m3的部分 | 2元/m3 |
超出6 m3但不超出10 m3的部分 | 4元/m3 |
超出10 m3的部分 | 8元/m3 |
注:水费按月结算. | |
(1)填空:若该户居民2月份用水4 m3 , 则应收水费元;
(2)若该户居民3月份用水a m3(其中6<a<10),则应收水费多少元?(用含a的整式表示并化简)
(3)若该户居民4,5月份共用水15 m3(5月份用水量超过了4月份),设4月份用水x m3 , 求该户居民4,5月份共交水费多少元?(用含x的整式表示并化简)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践
问题情境
在综合与实践课上,老师让同学们以“菱形纸片的剪拼”为主题开展数学活动,如图1,将一张菱形纸片ABCD(∠BAD>90°)沿对角线AC剪开,得到△ABC和△ACD.
操作发现
(1)将图1中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=∠BAC,得到如图2所示的△AC′D,分别延长BC和DC′交于点E,则四边形ACEC′的形状是 ;
(2)创新小组将图1中的△ACD以A为旋转中心,按逆时针方向旋转角α,使α=2∠BAC,得到如图3所示的△AC′D,连接DB,C′C,得到四边形BCC′D,发现它是矩形,请你证明这个结论;
实践探究
(3)缜密小组在创新小组发现结论的基础上,量得图3中BC=13cm,AC=10cm,然后提出一个问题:将△AC′D沿着射线DB方向平移acm,得到△A′C′D′,连接BD′,CC′,使四边形BCC′D恰好为正方形,求a的值,请你解答此问题;
(4)请你参照以上操作,将图1中的△ACD在同一平面内进行一次平移,得到△A′C′D,在图4中画出平移后构造出的新图形,标明字母,说明平移及构图方法,写出你发现的结论,不必证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)22+(﹣4)+(﹣2)+4
(2)(﹣ ![]() +1
+1 ![]() ﹣
﹣ ![]() )×(﹣24)
)×(﹣24)
(3)3﹣6÷(﹣2)×|﹣ ![]() |
|
(4)2a﹣(3b﹣a)+b
(5)3(x2﹣y2)+(y2﹣z2)﹣2(z2﹣y2)
(6)(﹣ ![]() )×(﹣4)2﹣0.25×(﹣5)×(﹣4)3 .
)×(﹣4)2﹣0.25×(﹣5)×(﹣4)3 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两班举行电脑汉字输入比赛,参赛学生每分钟输入汉字的个数统计结果如表:某同学分析表后得出如下结论:
班级 | 人数 | 中位数 | 方差 | 平均字数 |
甲 | 55 | 149 | 191 | 135 |
乙 | 55 | 151 | 110 | 135 |
①甲、乙两班学生成绩平均水平相同;
②乙班优秀的人数多于甲班优秀的人数(每分钟输入汉字≥150个为优秀);
③甲班成绩的波动比乙班小.上述结论正确的是( )
A. ①②③ B. ①② C. ①③ D. ②③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com