
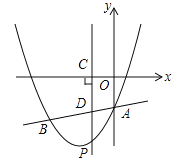
【题目】如图,抛物线![]() 与直线
与直线![]() 交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
交于A、B两点,其中点A在y轴上,点B坐标为(﹣4,﹣5),点P为y轴左侧的抛物线上一动点,过点P作PC⊥x轴于点C,交AB于点D.
(1)求抛物线的解析式;
(2)以O,A,P,D为顶点的平行四边形是否存在?如存在,求点P的坐标;若不存在,说明理由.
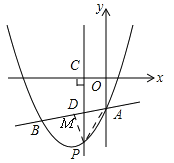
(3)当点P运动到直线AB下方某一处时,过点P作PM⊥AB,垂足为M,连接PA使△PAM为等腰直角三角形,请直接写出此时点P的坐标.
【答案】(1)![]() ;(2)P(
;(2)P(![]() ,
,![]() ),(﹣1,
),(﹣1,![]() ),(﹣3,
),(﹣3,![]() );(3)P(
);(3)P(![]() ,
,![]() ).
).
【解析】
试题分析:(1)先确定出点A坐标,然后用待定系数法求抛物线解析式;
(2)先用m表示出PD,当PD=OA=3,故存在以O,A,P,D为顶点的平行四边形,得到![]() ,分两种情况进行讨论计算即可;
,分两种情况进行讨论计算即可;
(3)由△PAM为等腰直角三角形,得到∠BAP=45°,从而求出直线AP的解析式,最后求出直线AP和抛物线的交点坐标即可.
试题解析:(1)∵直线![]() 交于A、B两点,其中点A在y轴上,∴A(0,﹣3),∵B(﹣4,﹣5),∴
交于A、B两点,其中点A在y轴上,∴A(0,﹣3),∵B(﹣4,﹣5),∴![]() ,∴
,∴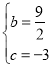 ,∴抛物线解析式为
,∴抛物线解析式为![]() ;
;
(2)存在,设P(m,![]() ),(m<0),∴D(m,
),(m<0),∴D(m,![]() ),∴PD=
),∴PD=![]() .
.
∵PD∥AO,∴当PD=OA=3,故存在以O,A,P,D为顶点的平行四边形,∴![]() ;
;
①当![]() 时,∴
时,∴![]() =
=![]() ,
,![]() =
=![]() (舍),∴
(舍),∴![]() =
=![]() ,∴P(
,∴P(![]() ,
,![]() );
);
②当![]() 时,∴
时,∴![]() =﹣1,
=﹣1,![]() =﹣3.
=﹣3.
Ⅰ、m1=﹣1,∴![]() =
=![]() ,∴P(﹣1,
,∴P(﹣1,![]() );
);
Ⅱ、m2=﹣3,∴![]() =
=![]() ,∴P(﹣3,
,∴P(﹣3,![]() );
);
∴点P的坐标为(![]() ,
,![]() ),(﹣1,
),(﹣1,![]() ),(﹣3,
),(﹣3,![]() );
);
(3)如图,∵△PAM为等腰直角三角形,∴∠BAP=45°,∵直线AP可以看做是直线AB绕点A逆时针旋转45°所得,设直线AP解析式为y=kx﹣3,∵直线AB解析式为![]() ,∴k=
,∴k=![]() =3,∴直线AP解析式为y=3x﹣3,联立:
=3,∴直线AP解析式为y=3x﹣3,联立: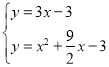 ,∴
,∴![]() =0(舍),
=0(舍),![]() =
=![]() ;
;
当x=![]() 时,y=
时,y=![]() ,∴P(
,∴P(![]() ,
,![]() ).
).


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
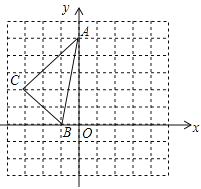
【题目】((2016四川省巴中市)如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法不正确的是( )
A.一组邻边相等的矩形是正方形
B.对角线互相垂直的矩形是正方形
C.对角线相等的菱形是正方形
D.有一组邻边相等、一个角是直角的四边形是正方形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() (m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线
(m<0)与x轴交于点A、B(点A在点B的左侧),该抛物线的对称轴与直线![]() 相交于点E,与x轴相交于点D,点P在直线
相交于点E,与x轴相交于点D,点P在直线![]() 上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
上(不与原点重合),连接PD,过点P作PF⊥PD交y轴于点F,连接DF.
(1)如图①所示,若抛物线顶点的纵坐标为![]() ,求抛物线的解析式;
,求抛物线的解析式;
(2)求A、B两点的坐标;
(3)如图②所示,小红在探究点P的位置发现:当点P与点E重合时,∠PDF的大小为定值,进而猜想:对于直线![]() 上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.
上任意一点P(不与原点重合),∠PDF的大小为定值.请你判断该猜想是否正确,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.三角形三条角平分线的交点是三角形的重心
B.三角形的一条角平分线把该三角形分成面积相等的两部分
C.三角形的中线、角平分线、高都是线段
D.三角形的三条高都在三角形内部
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现代互联网技术的广泛应用,催生了快递行业的高速发展.小明计划给朋友快递一部分物品,经了解有甲、乙两家快递公司比较合适.甲公司表示:快递物品不超过1千克的,按每千克22元收费;超过1千克,超过的部分按每千克15元收费.乙公司表示:按每千克16元收费,另加包装费3元.设小明快递物品x千克.
(1)请分别写出甲、乙两家快递公司快递该物品的费用y(元)与x(千克)之间的函数关系式;
(2)小明选择哪家快递公司更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com