
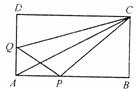
如图,在矩形ABCD中,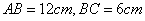 ,点P沿AB边从点A开始向点B以
,点P沿AB边从点A开始向点B以 的速度移动,点Q沿DA边从点D开始向A以
的速度移动,点Q沿DA边从点D开始向A以 的速度移动.如果P、Q同时出发,用
的速度移动.如果P、Q同时出发,用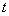 秒表示移动的时间
秒表示移动的时间 ),那么:
),那么:
(1)当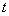 为何值时,△QPA为等腰直角三角形?
为何值时,△QPA为等腰直角三角形?
(2)对四边形QAPC的面积,提出一个与计算结果有关的结论.
(3)当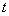 为何值时,以点Q、
为何值时,以点Q、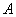 、
、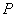 为顶点的三角形与△ABC相似?
为顶点的三角形与△ABC相似?
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
下列命题是真命题的是( )
A、三点确定一个圆
B、平行四边形既是轴对称图形又是中心对称图形
C、对角线相等且互相平分的四边形是矩形
D、有两边和一角对应相等的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
已知一元二次方程x2-(2k+1)x+k2+k=0 .
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB、AC的长是这个方程的两个实数根,第三边BC的长为5.
当△ABC是等腰三角形时,求k的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com