
【题目】某商场用14500元购进甲、乙两种矿泉水共500箱,矿泉水的成本价与销售价如表(二)所示:

求:(1)购进甲、乙两种矿泉水各多少箱?
(2)该商场售完这500箱矿泉水,可获利多少元?
【答案】(1)购进甲种矿泉水300箱,购进乙种矿泉水200箱;(2)该商场售完这500箱矿泉水,可获利5600元.
【解析】
(1)设购进甲种矿泉水x箱,购进乙种矿泉水y箱,根据题意,列出二元一次方程组并解方程即可;
(2)先求出这500箱矿泉水的总售价,再减去总成本即可求出总利润.
解:(1)设购进甲种矿泉水x箱,购进乙种矿泉水y箱
根据题意可得:![]()
解得:![]()
答:购进甲种矿泉水300箱,购进乙种矿泉水200箱.
(2)这500箱矿泉水的总售价为:300×35+200×48=20100(元)
∴该商场售完这500箱矿泉水,可获利20100-14500=5600(元)
答:该商场售完这500箱矿泉水,可获利5600元.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】我们都知道无限不循环小数是无理数,而无限循环小数是可以化成分数的,例如![]() (
(![]() 为循环节)是可以化成分数的,方法如下:
为循环节)是可以化成分数的,方法如下:
令![]() ①
①
则![]() ②
②
②-①得:![]() ,即
,即![]() ,解得
,解得![]()
请你阅读上面材料完成下列问题:
(1)![]() 化成分数是 .
化成分数是 .
(2)![]() 化成分数是 .
化成分数是 .
(3)请你将![]() 化成分数(写出过程)
化成分数(写出过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴上表示数![]() 的点与原点的距离叫做数
的点与原点的距离叫做数![]() 的绝对值,记作
的绝对值,记作![]() .数轴上表示数
.数轴上表示数![]() 的点与表示数
的点与表示数![]() 的点的距离记作
的点的距离记作![]() ,如
,如![]() 表示数轴上表示数3的点与表示数5的点的距离,
表示数轴上表示数3的点与表示数5的点的距离,![]() 表示数轴上表示数3的点与表示数-5的点的距离,
表示数轴上表示数3的点与表示数-5的点的距离,![]() 表示数轴上表示数
表示数轴上表示数![]() 的点与表示数3的点的距离.
的点与表示数3的点的距离.
![]()
根据以上材料回答下列问题:(将结果直接填写在答题卡相应位置,不写过程)
(1)若![]() ,则
,则![]() ________,若
________,若![]() ,则
,则![]() ___________;
___________;
(2)若![]() ,则
,则![]() 能取到的最小值是_________,最大值是_________;
能取到的最小值是_________,最大值是_________;
(3)关于![]() 的式子
的式子![]() 的取值范围是_________.
的取值范围是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】程大位是我国明朝商人,珠算发明家,他60岁时完成的《直指算法综宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法,书中有如下问题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚得几丁,意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完,大、小和尚各有多少人,则小和尚有__________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
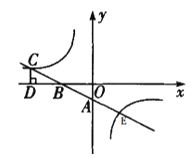
【题目】如图,一次函数y=![]() x-1的图象与坐标轴分别交于A、B两点,与反比例函数y=
x-1的图象与坐标轴分别交于A、B两点,与反比例函数y=![]() 的图象在第二象限的交点为点C,CD⊥x轴,垂足为点D,若C点横坐标为-4,
的图象在第二象限的交点为点C,CD⊥x轴,垂足为点D,若C点横坐标为-4,
(1)反比例函数的关系式及E点坐标;
(2)利用图像,当x<0时,写出![]()
![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的袋中装有5个只有颜色不同的球,其中3个黄球,2个黑球.
(1)求从袋中同时摸出的两个球都是黄球的概率;
(2)现将黑球和白球若干个(黑球个数是白球个数的2倍)放入袋中,搅匀后,若从袋中摸出一个球是黑球的概率是![]() ,求放入袋中的黑球的个数.
,求放入袋中的黑球的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
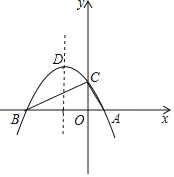
【题目】如图,抛物线y=﹣![]() x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
x2+bx+2与x轴交于A,B两点,与y轴交于C点,且点A的坐标为(1,0).
(1)求抛物线的解析式及顶点D的坐标;
(2)判断△ABC的形状,并证明你的结论;
(3)点M是抛物线对称轴上的一个动点,当△ACM的周长最小时,求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
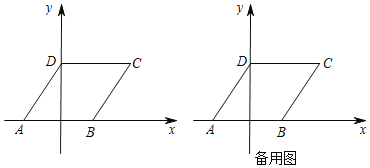
【题目】如图,ABCD在平面直角坐标系中,点A(﹣2,0),点B(2,0),点D(0,3),点C在第一象限.
(1)求直线AD的解析式;
(2)若E为y轴上的点,求△EBC周长的最小值;
(3)若点Q在平面直角坐标系内,点P在直线AD上,是否存在以DP,DB为邻边的菱形DBQP?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com