
 时,求出此二次函数的解析式;
时,求出此二次函数的解析式;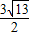 ?若存在求出P点坐标,若不存在请说明理由.
?若存在求出P点坐标,若不存在请说明理由.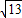 ,可得:(x1-x2)2=13,即可得(x1+x2)2-4x1•x2=13,继而求得a的值;
,可得:(x1-x2)2=13,即可得(x1+x2)2-4x1•x2=13,继而求得a的值;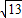 ,△PAB的面积为
,△PAB的面积为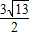 ,即可求得y的值,继而求得P点坐标.
,即可求得y的值,继而求得P点坐标.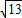 ,
,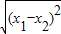 =
=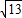 .
.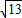 ,
,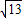 ,
, AB•|y|=
AB•|y|=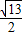 ,
,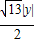 =
=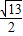


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com