
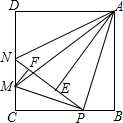
 如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.
如图,在正方形ABCD中,AB=4,P是BC边上一动点(不含B,C两点),将△ABP沿直线AP翻折,点B落在点E处,在CD上有一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.分析 发现:先证明∠MPA=90°,然后依据同角的余角相等可证明∠CPM=∠PAB,结合条件∠C=∠B=90°,可证明量三角形相似;
思考:设PB=x,则CP=4-x,依据相似三角形的性质可得到CM=$\frac{1}{4}$x(4-x),作MG⊥AB于G,依据勾股定理可得到AM=$\sqrt{16+A{G}^{2}}$,则AG最小值时,AM最小,然后由AG=AB-BG=AB-CM得到AG与x的函数关系,依据二次函数的性质可求得当x=2时,AG最小值=3;
探究:依据全等三角形的性质和翻折的性质可得到∠PAB=∠DAN=∠EAP=∠EAN=22.5°,在AB上取一点K使得AK=PK,设PB=z.然后可证明△BPK为等腰直角三角形,故此得到PB=BK=z,AK=PK=$\sqrt{2}$z,最后依据AK+BK=4列出关于z的方程求解即可.
解答 解:发现.∵∠APB=∠APE,∠MPC=∠MPN,∠CPN+∠NPB=180°,
∴2∠NPM+2∠APE=180°,
∴∠MPN+∠APE=90°,
∴∠APM=90°,
∵∠CPM+∠APB=90°,∠APB+∠PAB=90°,
∴∠CPM=∠PAB.
又∵∠C=∠B=90°,
∴△CMP∽△BPA.
思考:设PB=x,则CP=4-x.
∵△CMP∽△BPA,
∴$\frac{PB}{CM}=\frac{AB}{PC}$,
∴CM=$\frac{1}{4}$x(4-x).
如图1所示:作MG⊥AB于G.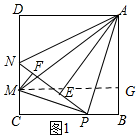
∵AM=$\sqrt{M{G}^{2}+A{G}^{2}}$=$\sqrt{16+A{G}^{2}}$,
∴AG最小值时,AM最小.
∵AG=AB-BG=AB-CM=4-$\frac{1}{4}$x(4-x)=$\frac{1}{4}$(x-2)2+3,
∴x=2时,AG最小值=3.
∴AM的最小值=$\sqrt{16+9}$=5.
探究:∵△ABP≌△ADN,
∴∠PAB=∠DAN,AP=AN,
又∵∠PAB=∠EAP,∠AEP=∠B=90°,
∴∠EAP=∠EAN,
∴∠PAB=∠DAN=∠EAP=∠EAN=22.5°.
如图2:在AB上取一点K使得AK=PK,设PB=z.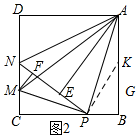
∴∠KPA=∠KAP=22.5°,
∵∠PKB=∠KPA+∠KAP=45°,
∴∠BPK=∠BKP=45°,
∴PB=BK=z,AK=PK=$\sqrt{2}$z,
∴z+$\sqrt{2}$z=4,
∴z=4$\sqrt{2}$-4.
∴PB=4$\sqrt{2}$-4.
点评 本题主要考查的是相似三角形的综合应用,解答本题主要应用了相似三角形的性质和判定、翻折的性质、勾股定理、等腰直角三角形的性质和判定,二次函数的最值,列出AG的长与x的函数关系式是解答问题(2)的关键;截取AK=PK,构造出等腰直角△PBK,然后依据题意列出关于z的方程是解答问题(3)的关键.


科目:初中数学 来源: 题型:选择题
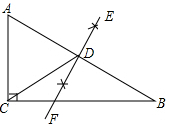 如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )
如图,在Rt△ABC中,∠ACB=90°,BC=12,AC=5,分别以点A,B为圆心,大于线段AB长度的一半为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连接CD,则△ACD的周长为( )| A. | 13 | B. | 17 | C. | 18 | D. | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 明天太阳从西边升起 | |
| B. | 篮球队员在罚球线上投篮一次,未投中 | |
| C. | 抛出一枚硬币,落地后正面朝上 | |
| D. | 实心铁球投入水中会沉入水底 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com