
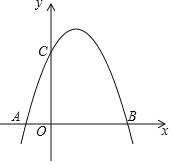
【题目】如图,是将抛物线![]() 平移后得到的抛物线,其对称轴为
平移后得到的抛物线,其对称轴为![]() ,与
,与![]() 轴的一个交点为
轴的一个交点为![]() ,另一交点为
,另一交点为![]() ,与
,与![]() 轴交点为
轴交点为![]() .
.
(1)求抛物线的函数表达式;
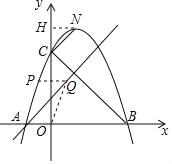
(2)若点![]() 为抛物线上一点,且
为抛物线上一点,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)点![]() 是抛物线上一点,点
是抛物线上一点,点![]() 是一次函数
是一次函数![]() 的图象上一点,若四边形
的图象上一点,若四边形![]() 为平行四边形,这样的点
为平行四边形,这样的点![]() 是否存在?若存在,分别求出点
是否存在?若存在,分别求出点![]() 的坐标,若不存在,说明理由.
的坐标,若不存在,说明理由.
【答案】(1)y=﹣x2+2x+3(2)(1,4)(3)P、Q的坐标是(0,3),(1,3)或(![]() ,
,![]() )、(
)、(![]() ,
,![]() )
)
【解析】
试题分析:(1)已知抛物线的对称轴,因而可以设出顶点式,利用待定系数法求函数解析式;
(2)首先求得B和C的坐标,易证△OBC是等腰直角三角形,过点N作NH⊥y轴,垂足是H,设点N纵坐标是(a,﹣a2+2a+3),根据CH=NH即可列方程求解;
(3)四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,设P(t,﹣t2+2t+3),代入y=![]() x+
x+![]() ,即可求解.
,即可求解.
试题解析:(1)设抛物线的解析式是y=﹣(x﹣1)2+k.
把(﹣1,0)代入得0=﹣(﹣1﹣1)2+k,
解得k=4,
则抛物线的解析式是y=﹣(x﹣1)2+4,即y=﹣x2+2x+3;
(2)在y=﹣x2+2x+3中令x=0,则y=3,即C的坐标是(0,3),OC=3.
∵B的坐标是(3,0),
∴OB=3,
∴OC=OB,则△OBC是等腰直角三角形.
∴∠OCB=45°,
过点N作NH⊥y轴,垂足是H.
∵∠NCB=90°,
∴∠NCH=45°,
∴NH=CH,
∴HO=OC+CH=3+CH=3+NH,
设点N纵坐标是(a,﹣a2+2a+3).
∴a+3=﹣a2+2a+3,
解得a=0(舍去)或a=1,
∴N的坐标是(1,4);
(3)∵四边形OAPQ是平行四边形,则PQ=OA=1,且PQ∥OA,
设P(t,﹣t2+2t+3),代入y=![]() x+
x+![]() ,则﹣t2+2t+3=
,则﹣t2+2t+3=![]() (t+1)+
(t+1)+![]() ,
,
整理,得2t2﹣t=0,
解得t=0或![]() .
.
∴﹣t2+2t+3的值为3或![]() .
.
∴P、Q的坐标是(0,3),(1,3)或(![]() ,
,![]() )、(
)、(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】把点M(-2,1)向右平移3个单位长度,再向下平移2个单位长度后得到点N,则点N的坐标为( )
A.(-4,4)B.(-5,3)C.(1,-1)D.(-5,-1)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一些汉字的美术字中,有的是轴对称图形.下面五个词中“自由 平等 民主 敬业 友善”可以看作轴对称图形的汉字有个.( )
A.2个
B.3个
C.4个
D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在践行社会主义核心价值观活动中,共评选出各级各类“湖北好人”45 000多名.45 000这个数用科学记数法表示为( )
A.4.5×103
B.4.5×104
C.4.5×105
D.0.45×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=8cm,BC=6cm,点D以每秒1cm的速度从点C出发,沿边CA往A运动,当运动到点A时停止。若设点D运动的时间为t秒,则当t=时,△CBD是等腰三角形。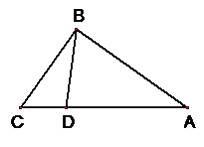
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为筹备班级的初中联欢会,班委会经过讨论决定在苹果、桔子、香蕉、梨四种水管中选出一种购买,班长对全班学生爱吃那种水果做了调查,则最终在决定购买哪种水果时,下面的调查数据最值得关注的是( )
A.众数B.平均数C.中位数D.方差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com