
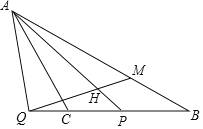
【题目】如图,已知等腰△ABC,∠ACB=120°,P是线段CB上一动点(与点C,B不重合),连接AP,延长BC至点Q,使得∠PAC=∠QAC,过点Q作射线QH交线段AP于H,交AB于点M,使得∠AHQ=60°.
(1)若∠PAC=α,求∠AMQ的大小(用含α的式子表示);
(2)用等式表示线段QC和BM之间的数量关系,并证明.
【答案】(1)∠AMQ=30°+α;(2)BM![]() CQ,证明见解析.
CQ,证明见解析.
【解析】
(1)根据等腰△ABC,∠ACB=120,得到∠B=∠CAB=30°,由∠ACQ=60°.
∠AHQ=60°,可得∠AGH=∠QGC,则有∠MQB=∠PAC=α,利用三角形的外角的性质,可知∠AMQ=30°+α;
(2)过点M作ME∥AC,交BQ于点E,根据∠PAC=∠QAC=α,∠QAM=∠QMA=30°+α,可得QA=QM,∠ACQ=∠MEQ=60,利用AAS可证△QAC≌△MQE,可以得出EM=EB,设EN=x,则BE=EM=2x,BN![]() x,可得BM=2
x,可得BM=2![]() x,CQ=EM=2x,可求出 BM
x,CQ=EM=2x,可求出 BM![]() CQ.
CQ.
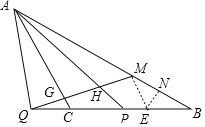
(1)如图
∠ACB=120°,AC=BC,
∴∠B=∠CAB=30°,∠ACQ=60°.
∵∠AHQ=60°.
∵∠AGH=∠QGC,∴∠MQB=∠PAC=α
∠AMQ=∠B+∠MQB=30°+α;
(2)如图,

过点M作ME∥AC,交BQ于点E,
∵∠PAC=∠QAC=α,
∴∠QAM=∠QMA=30°+α,
∴QA=QM
∴∠ACQ=∠MEQ=60°,∠QAC=∠MQE,
∴△QAC≌△MQE(AAS),∴CQ=EM
∵∠B=30°,∴∠EMB=30°,∴EM=EB,
作EN⊥BM于点N,
设EN=x,则BE=EM=2x,BN![]() x,∴BM=2
x,∴BM=2![]() x,
x,
CQ=EM=2x,∴BM![]() CQ.
CQ.


科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)甲说:该二次函数的图象必定经过点![]() .乙说:若图象的顶点在x轴上,则
.乙说:若图象的顶点在x轴上,则![]() ,你觉得他们的结论对吗?请说明理由;
,你觉得他们的结论对吗?请说明理由;
(2)若抛物线经过![]() ,
,![]() ,求证
,求证![]() ;
;
(3)甲问乙:“我取的k是一个整数,画出它的图象后发现抛物线与x轴的一个交点在y轴右侧,一个交点在原点和![]() 之间,你知道k等于几吗?并求出k的值.
之间,你知道k等于几吗?并求出k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=2![]() ,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.
,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB折叠后,点A落在第一象限内的点C处.

(1)求经过点O,C,A三点的抛物线的解析式.
(2)若点M是抛物线上一点,且位于线段OC的上方,连接MO、MC,问:点M位于何处时三角形MOC的面积最大?并求出三角形MOC的最大面积.
(3)抛物线上是否存在一点P,使∠OAP=∠BOC?若存在,请求出此时点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,长度为6千米的国道![]() 两侧有
两侧有![]() ,
,![]() 两个城镇,从城镇到公路分别有乡镇公路连接,连接点为
两个城镇,从城镇到公路分别有乡镇公路连接,连接点为![]() 和
和![]() ,其中
,其中![]() 、
、![]() 之间的距离为2千米,
之间的距离为2千米,![]() 、
、![]() 之间的距离为1千米,
之间的距离为1千米,![]() 、
、![]() 之间的乡镇公路长度为2.3千米,
之间的乡镇公路长度为2.3千米,![]() 、
、![]() 之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道
之间的乡镇公路长度为3.2千米,为了发展乡镇经济,方便两个城镇的物资输送,现需要在国道![]() 上修建一个物流基地
上修建一个物流基地![]() ,设
,设![]() 、
、![]() 之间的距离为
之间的距离为![]() 千米,物流基地
千米,物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和为
两个城镇的距离之和为![]() 干米,以下是对函数
干米,以下是对函数![]() 随自变量
随自变量![]() 的变化规律进行的探究,请补充完整.
的变化规律进行的探究,请补充完整.
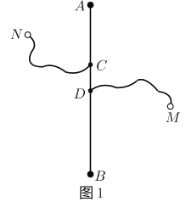
(1)通过取点、画图、测量,得到![]() 与
与![]() 的几组值,如下表:
的几组值,如下表:
| 0 | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 | 6.0 |
| 10.5 | 8.5 | 6.5 | 10.5 | 12.5 |
(2)如图2,建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象.
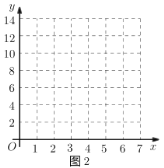
(3)结合画出的函数图象,解决问题:
①若要使物流基地![]() 沿公路到
沿公路到![]() 、
、![]() 两个城镇的距离之和最小,则物流基地
两个城镇的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.
②如右图,有四个城镇![]() 、
、![]() 、
、![]() 、
、![]() 分别位于国道
分别位于国道![]() 两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地
两侧,从城镇到公路分别有乡镇公路连接,若要在国道上修建一个物流基地![]() ,使得
,使得![]() 沿公路到
沿公路到![]() 、
、![]() 、
、![]() 、
、![]() 的距离之和最小,则物流基地
的距离之和最小,则物流基地![]() 应该修建在何处?(写出所有满足条件的位置)
应该修建在何处?(写出所有满足条件的位置)
答:__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠C=90°,AD⊥DB,点E为AB的中点,DE∥BC.
(1)求证:BD平分∠ABC;
(2)连接EC,若∠A=30°,DC![]() ,求EC的长.
,求EC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小李经营一家水果店,某日到水果批发市场批发一种水果.经了解,一次性批发这种水果不得少于![]() ,超过
,超过![]() 时,所有这种水果的批发单价均为3元
时,所有这种水果的批发单价均为3元![]() .图中折线表示批发单价
.图中折线表示批发单价![]() (元
(元![]() )与质量
)与质量![]() 的函数关系.
的函数关系.
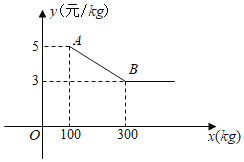
(1)求图中线段![]() 所在直线的函数表达式;
所在直线的函数表达式;
(2)小李用800元一次可以批发这种水果的质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() ,点
,点![]() 为
为![]() 上的一点,在
上的一点,在![]() 同侧作正方形
同侧作正方形![]() ,正方形
,正方形![]() 分别为对角线
分别为对角线![]() 的中点,连结
的中点,连结![]() 当点
当点![]() 沿着线段
沿着线段![]() 由点
由点![]() 向点
向点![]() 方向上移动时,四边形
方向上移动时,四边形![]() 的面积变化情况为( )
的面积变化情况为( )
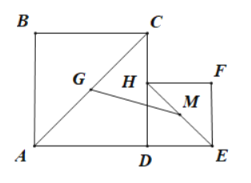
A.不变B.先减小后增大
C.先增大后减小D.一直减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某小区游泳馆夏季推出两种收费方式.方式一:先购买会员证,会员证200元,只限本人当年使用,凭证游泳每次需另付费10元:方式二:不购买会员证,每次游泳需付费20元.
(1)若甲计划今年夏季游泳的费用为500元,则选择哪种付费方式游泳次数比较多?
(2)若乙计划今年夏季游泳的次数超过15次,则选择哪种付费方式游泳花费比较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点A(3,0)和点B(2,3),过点A的直线与y轴的负半轴相交于点C,且tan∠CAO=![]() .
.
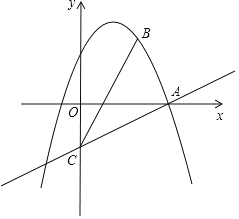
(1)求这条抛物线的表达式及对称轴;
(2)联结AB、BC,求∠ABC的正切值;
(3)若点D在x轴下方的对称轴上,当S△DBC=S△ADC时,求点D的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com