练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    11．因式分解：3x2-27=3（x+3）（x-3）．

    分析 先提取公因式3，再根据平方差公式进行二次分解即可求得答案．注意分解要彻底．

    解答 解：原式=3（x2-9）=3（x+3）（x-3），
    故答案为3（x+3）（x-3）．

    点评 本题考查了提公因式法，公式法分解因式，提取公因式后利用平方差公式进行二次分解，注意分解要彻底．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

    1．近似数3.14×104的精确到（　　）
    A．个位B．百位C．百分位D．千位

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．我州某景点的门票销售分两类：一类为散客门票，价格为80元/张；另一类为团体门票（一次性购买10张及以上），每张门票价格在散客门票价格基础上打8折，某班级部分同学要去该景点游玩，设参加旅游的人数为x，购买门票需要y元．
    （1）如果每人分别买票，求y与x的函数解析式；
    （2）如果购买团体票，求y与x的函数解析式，并写出自变量的范围；
    （3）请你设计一种比较省钱的购票方案．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

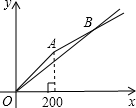    19．甲、乙两家商店以同样价格销售相同的商品，某次促销活动中，它们的优惠方案分别为：甲店，所有商品一律八折优惠；乙店，一次性购物中超过200元后的价格部分打六折．设商品原价为x元（x＞0），购物应付金额为y元．
    （1）求在乙商店购物时y2与x之间的函数关系；
    （2）两种购物方式对应的函数如图所示，求出交点B的坐标；
    （3）根据图象，请直接写出本次促销活动汇总选择哪家商店购物更优惠．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    6．为了配合“绿色盐城”建设，展示“射阳风景”，某社区计划对面积为3600m2的区域进行绿化，经投标，由甲、乙两个工程队来完成，已知甲队每天能完成绿化的面积是乙队每天能完成绿化面积的2倍，并且在独立完成面积为600m2区域的绿化时，甲队比乙队少用3天．
    （1）求甲、乙两工程队每天能完成绿化的面积；
    （2）设甲工程队施工x天，乙工程队施工y天，刚好完成绿化任务，求y与x的函数解析式；
    （3）若甲队每天绿化费用是0.8万元，乙队每天绿化费用为0.3万元，且甲乙两队施工的总天数不超过25天，则如何安排甲乙两队施工的天数，使施工总费用最低？并求出最低费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．分解因式：x3-4x2+4x=x（x-2）2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

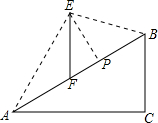    3．如图，在坡度i=1：$\sqrt{3}$的斜坡AB上立有一电线杆EF，工程师在点A处测得E的仰角为60°，沿斜坡前进20米到达B，此时测得点E的仰角为15°，现要在斜坡AB上找一点P，在P处安装一根拉绳PE来固定电线杆，以使EF保持竖直，为使拉绳PE最短，则FP的长度约为（　　）（参考数据：$\sqrt{2}$≈1.414，$\sqrt{3}$≈1.732）
    A．3.7米B．3.9米C．4.2米D．5.7米

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，抛物线y=-x2+2x+3与x轴交于A，B两点，与y轴交于点C，点D，C关于抛物线的对称轴对称，直线AD与y轴相交于点E．
    （1）求直线AD的解析式；
    （2）如图1，直线AD上方的抛物线上有一点F，过点F作FG⊥AD于点G，作FH平行于x轴交直线AD于点H，求△FGH周长的最大值；
    （3）如图2，点M是抛物线的顶点，点P是y轴上一动点，点Q是坐标平面内一点，四边形APQM是以PM为对角线的平行四边形，点Q′与点Q关于直线AM对称，连接M Q′，P Q′．当△PM Q′与□APQM重合部分的面积是?APQM面积的$\frac{1}{4}$时，求?APQM面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列各式中，能满足完全平方公式进行因式分解的是（　　）
    A．2x2-4x+6B．x2+2x+4C．x2-y2+2xyD．4x2-12xy+9y2

    查看答案和解析>>

    同步练习册答案