
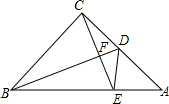
 已知等腰Rt△ABC,BD是AC边上的中线,∠CBD=∠ACE.求证:∠CDF=∠ADE.
已知等腰Rt△ABC,BD是AC边上的中线,∠CBD=∠ACE.求证:∠CDF=∠ADE. 分析 在BD上截取BG=CE,利用SAS证明△ACE与△CBG全等,再进而证明△ADE与△CDG全等即可.
解答 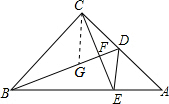 证明:在BD上截取BG=CE,连接CG,如图:
证明:在BD上截取BG=CE,连接CG,如图:
在△ACE与△CBG中,
$\left\{\begin{array}{l}{BC=AC}\\{∠CBD=∠ACE}\\{BG=CE}\end{array}\right.$,
∴△ACE≌△CBG(SAS),
∴CG=AE,∠BCG=∠A=45°,
∴∠GCD=45°,
在△ADE与△CDG中,
$\left\{\begin{array}{l}{CD=AD}\\{∠GCD=∠A=45°}\\{CG=AE}\end{array}\right.$,
∴△ADE≌△CDG(SAS),
∴∠CDF=∠ADE.
点评 此题考查全等三角形的判定和性质,关键是在BD上截取BG=CE,利用SAS证明△ACE与△CBG全等.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
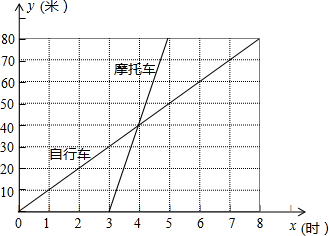 如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象.两地间的距离是80千米.请你根据图象回答或解决下面的问题:
如图表示一骑自行车者和一骑摩托车者沿相同路线由甲地到乙地行驶过程的函数图象.两地间的距离是80千米.请你根据图象回答或解决下面的问题:查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 4017 | B. | 4018 | C. | 4019 | D. | 4020 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
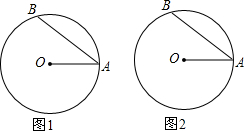 如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.
如图,⊙O的半径OA=5cm,AB是弦,∠OAB=30°,现有一动点C从A出发,沿弦AB运动到B,再从B沿劣弧BA回到点A.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
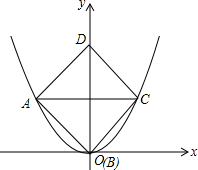 已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.
已知边长为2的正方形在平面直角坐标系中的位置如图所示,其顶点A、B、C在图中的抛物线上,则此抛物线的解析式为:$\frac{\sqrt{2}}{2}$x2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 圆周率π是无限不循环小数,它不是有理数 | |
| B. | 负整数与负分数统称为负有理数 | |
| C. | 正有理数与负有理数组成全体有理数 | |
| D. | $\frac{20}{5}$不是分数,而是整数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在同一坐标系中画出下列函数的图象:
在同一坐标系中画出下列函数的图象:| x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
| y=-x2 | … | … | |||||||||
| y=-(x+2)2 | … | … | |||||||||
| y=-(x-1)2 | … | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com