
分析 首先对括号内的式子通分相加,把除法化为乘法,计算乘法即可化简,然后解方程求得x的值,代入化简后 的式子求解.
解答 解:原式=$\frac{x-2}{(x+1)(x-1)}$÷$\frac{1-2x+(x+1)(x-1)}{x+1}$
=$\frac{x-2}{(x+1)(x-1)}$÷$\frac{1-2x+{x}^{2}-1}{x+1}$
=$\frac{x-2}{(x+1)(x-1)}$÷$\frac{x(x-2)}{x+1}$
=$\frac{x-2}{(x+1)(x-1)}$•$\frac{x+1}{x(x-2)}$
=$\frac{1}{x(x-1)}$.
解方程x2+x-6=0得x1=-3,x2=2.
当x=-3时,原式=$\frac{1}{-3×(-4)}$=$\frac{1}{12}$;
当x=2时,原式无意义.
点评 本题考查分式的化简求值,以及一元二次方程的解法,注意到分式有意义的条件是关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.
如图,已知∠MON=25°,矩形ABCD的边BC在OM上,对角线AC⊥ON.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
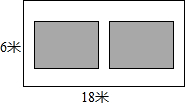 如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为1米.
如图,某小区有一块长为18米,宽为6米的矩形空地,计划在其中修建两块相同的矩形绿地,它们面积之和为60米2,两块绿地之间及周边留有宽度相等的人行通道,则人行道的宽度为1米.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种糖果 | 乙种糖果 | 丙种糖果 | |
| 单价(元/千克) | 15 | 20 | 25 |
| 千克(千克) | 30 | 40 | 30 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com