
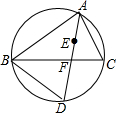
 如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D
如图,点E是△ABC的内心,AE的延长线与BC相交于点F,与△ABC的外接圆相交于点D分析 (1)先根据内心的性质得出∠BAD=∠CAD,再由圆周角定理得出∠CAD=∠CBD,故可得出∠BAD=∠CBD,进而可得出结论;
(2)连接BE,根据点E是△ABC的内心得出∠ABE=∠CBE.由∠CBD=∠BAD可得出∠BAD+∠ABE=∠CBE+∠CBD,进而可得出结论.
解答 (1)证明:∵点E是△ABC的内心,
∴∠BAD=∠CAD.
∵∠CAD=∠CBD,
∴∠BAD=∠CBD.
∵∠BDF=∠ADB,
∴△BFD∽△ABD;
(2)证明:连接BE,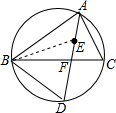
∵点E是△ABC的内心,
∴∠ABE=∠CBE.
又∵∠CBD=∠BAD,
∴∠BAD+∠ABE=∠CBE+∠CBD.
∵∠BAD+∠ABE=∠BED,∠CBE+∠CBD=∠DBE,即∠DBE=∠BED,
∴DE=DB.
点评 本题考查的是相似三角形的判定与性质,根据题意作出辅助线,利用三角形内心的性质求解是解答此题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )
如图,在Rt△ABC中,∠C=90°,AC=4,BC=7,点D在边BC上,CD=3,⊙A的半径长为3,⊙D与⊙A相交,且点B在⊙D外,那么⊙D的半径长r的取值范围是( )| A. | 1<r<4 | B. | 2<r<4 | C. | 1<r<8 | D. | 2<r<8 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
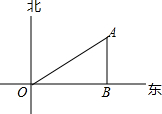 如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )
如图,小雅家(图中点O处)门前有一条东西走向的公路,经测得有一水塔(图中点A处)在距她家北偏东60°方向的500米处,那么水塔所在的位置到公路的距离AB是( )| A. | 250米 | B. | 250$\sqrt{3}$米 | C. | $\frac{500}{3}$$\sqrt{3}$米 | D. | 500$\sqrt{2}$米 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
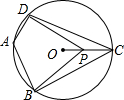 如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为80度(写出一个即可).
如图,四边形ABCD内接于⊙O,∠DAB=130°,连接OC,点P是半径OC上任意一点,连接DP,BP,则∠BPD可能为80度(写出一个即可).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | 6 | D. | 9 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 等级 | 人数/名 | 百分比 |
| 优秀 | 200 | 20% |
| 良好 | 600 | 60% |
| 及格 | 150 | 15% |
| 不及格 | 50 | a |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com