
分析 根据a、b互为相反数且均不为0,可得:a+b=0;c、d互为倒数,可得:cd=1;据此求出(a+b)×5+$\frac{b}{a}$-$\frac{2}{3}$cd的值是多少即可.
解答 解:∵a、b互为相反数且均不为0,
∴a+b=0,$\frac{b}{a}$=-1;
∵c、d互为倒数,
∴cd=1;
∴(a+b)×5+$\frac{b}{a}$-$\frac{2}{3}$cd
=0×5+(-1)-$\frac{2}{3}$×1
=-1$\frac{2}{3}$
故答案为:-1$\frac{2}{3}$.
点评 此题主要考查了代数式求值问题,要熟练掌握,求代数式的值可以直接代入、计算.如果给出的代数式可以化简,要先化简再求值.题型简单总结以下三种:①已知条件不化简,所给代数式化简;②已知条件化简,所给代数式不化简;③已知条件和所给代数式都要化简.


科目:初中数学 来源: 题型:选择题
| A. | 5×10-7毫米2 | B. | 5×10-8毫米2 | C. | 2×106毫米2 | D. | 2×107毫米2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
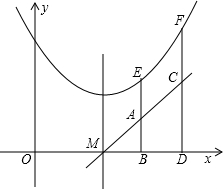 如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )
如图,点E(x1,y1),F(x2,y2)在抛物线y=ax2+bx+c上,且在该抛物线对称轴的同侧(点E在点F的左侧),过点E、F分别作x轴的垂线,分别交x轴于点B、D,交直线y=2ax+b于点A、C.设S为四边形ABDC的面积.则下列关系正确的是( )| A. | S=y2+y1 | B. | S=y2+2y1 | C. | S=y2-y1 | D. | S=y2-2y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
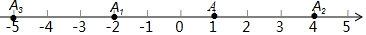 如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.
如图,在数轴上,点A表示1,现将点A沿数轴做如下移动,第一次点A向左移动3个单位长度到达点A1,第2次从点A1向右移动6个单位长度到达点A2,第3次从点A2向左移动9个单位长度到达点A3,…,按照这种移动规律进行下去,第n次移动到达点An,如果点An与原点的距离不小于50,那么n的最小值是33.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
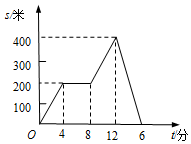 小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.
小明从家出发,外出散步,到一个公共阅报栏前看了一会儿报后,继续散步一段时间,然后回家.图中描述了小明在散步过程中到家的距离s(m)与散步所用时间t(min)之间的函数关系,则小明看报用了4min;小明返回家时的平均速度是100m/min.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.
如图,在△ABC中,AB=AC,D是BA延长线上的一点,点E是AC的中点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
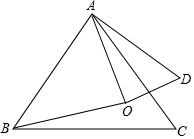 如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,
如图,点O是等边△ABC内一点,∠AOB=110°,∠BOC=α,将△BOC绕点C按顺时针方向旋转60°得△ADC,连接OD,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com