
【题目】在△ABC中,∠A=90°,点D在线段BC上,∠EDB=![]() ∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
∠C,BE⊥DE,垂足为E,DE与AB相交于点F.
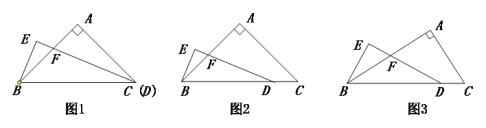
探究:当AB=AC且C,D两点重合时(如图1)探究:
(1)线段BE与FD之间的数量关系,直接写出结果 ;
(2)∠EBF= .
证明:当AB=AC且C,D不重合时,探究线段BE与FD的数量关系,并加以证明.
计算:当AB=![]() AC时,如图,求
AC时,如图,求![]() 的值 (用含
的值 (用含![]() 的式子表示).
的式子表示).
【答案】(1)BE=![]() FD;(2)22.5°,证明:BE=
FD;(2)22.5°,证明:BE=![]() FD,见解析;计算:
FD,见解析;计算:![]()
【解析】
探究:(1)首先延长CA与BE交于点G,根据∠EDB=![]() ∠C,BE⊥DE,判断出BE=EG=
∠C,BE⊥DE,判断出BE=EG=![]() BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=
BG;然后根据全等三角形的判定方法,判断出△ABG≌△ACF,即可判断出BG=CF=FD,再根据BE=![]() BG,可得BE=
BG,可得BE=![]() FD,据此判断即可;
FD,据此判断即可;
(2)根据(1)的结论易求得答案;
证明:过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H,仿照(1)的方法判断出△DEB≌△DEG和△GBH≌△FDH,即可推出结论;
计算:利用(2)的结论证得△GBH∽△FDH和△BHD∽△BAC,利用对应边成比例即可求得结论.
探究:(1)如图①,延长CA与BE交于点G,

∵∠EDB=![]() ∠C,
∠C,
∴∠EDB =∠EDG,
即CE是∠BCG的平分线,
又∵BE⊥DE,
∴BE=EG=![]() BG,
BG,
∵∠BED=∠BAD=90°,∠BFE=∠CFA,
∴∠EBF=∠ACF,
即∠ABG=∠ACF,
在△ABG和△ACF中,
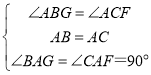 ,
,
∴△ABG≌△ACF,
∴BG=CF=FD,
又∵BE=![]() BG,
BG,
∴BE=![]() FD;
FD;
(2)∵AB=AC,∠A=90°,
∴∠ACB=45![]() ,
,
由(1)得CE是∠BCG的平分线,且∠EBF=∠ACF,
∴∠EBF=![]() ∠ACB=
∠ACB=![]() ;
;
证明:结论BE=![]() FD.
FD.
证明如下:
如图②,过点D作DG∥CA,与BE的延长线相交于点G,与AB相交于点H,

则∠GDB=∠C,∠BHD=∠A=90°=∠GHB.
∵∠EDB=![]() ∠C=
∠C=![]() ∠GDB=∠EDG,
∠GDB=∠EDG,
在△DEB和△DEG中,
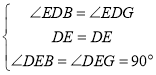 ,
,
∴△DEB≌△DEG,
∴BE=GE=![]() GB.
GB.
∵∠A=90°,AB=AC,
∴∠ABC=∠C=∠GDB,
∴HB=HD.
∵∠BED=∠BHD=90°, ∠BFE=∠DFH,
∴∠EBF=∠HDF,
在△GBH和△FDH中,
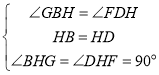 ,
,
∴△GBH≌△FDH,
∴GB=FD,
∴BE=![]() FD;
FD;
计算:∵△DEB≌△DEG,BE=![]() GB,∠BHD=∠BEF=90°,∠EBF=∠HDF,
GB,∠BHD=∠BEF=90°,∠EBF=∠HDF,
∴△GBH∽△FDH,
∴![]() ,即
,即![]() .
.
又∵DG∥CA,
∴△BHD∽△BAC,
∴![]() ,即
,即![]() .
.
∴![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,为了测量建筑物CD、EF的高度,在直线CE上选取观测点A、B,AC的距离为40米.从A、B测得建筑物的顶部D的仰角分别为51.34°、68.20°,从B、D测得建筑物的顶部F的仰角分别为64.43°、26.57°.
(1)求建筑物CD的高度;
(2)求建筑物EF的高度.
(参考数据:tan51.34°≈1.25,tan68.20°≈2.5,tan64.43°≈2,tan26.57°≈0.5)

查看答案和解析>>
科目:初中数学 来源: 题型:
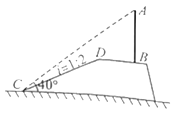
【题目】为积极宣传国家相关政策,某村在一山坡的顶端的平地上竖立一块宣传牌![]() .小明为测得宣传牌的高度,他站在山脚
.小明为测得宣传牌的高度,他站在山脚![]() 处测得宣传牌的顶端
处测得宣传牌的顶端![]() 的仰角为
的仰角为![]() ,已知山坡
,已知山坡![]() 的坡度
的坡度![]() ,山坡
,山坡![]() 的长度为
的长度为![]() 米,山坡顶端
米,山坡顶端![]() 与宣传牌底端
与宣传牌底端![]() 的水平距离为2米,求宣传牌的高度
的水平距离为2米,求宣传牌的高度![]() (精确到1米)
(精确到1米)
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
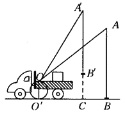
【题目】小刘同学在课外活动中观察吊车的工作过程,绘制了如图所示的平面图形.已知吊车吊臂的支点O距离地面的高度OO′=2米.当吊臂顶端由A点抬升至 A′点(吊臂长度不变)时,地面B处的重物(大小忽略不计)被吊至B′处,紧绷着的吊绳A′B′=AB.AB垂直地面 O′B于点B,A′B′垂直地面O′B于点C,吊臂长度OA′=OA=10米,且cosA![]() ,sinA′
,sinA′![]() .求此重物在水平方向移动的距离BC.
.求此重物在水平方向移动的距离BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
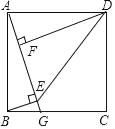
【题目】如图,正方形ABCD中,G为BC边上一点,BE⊥AG于E,DF⊥AG于F,连接DE.
(1)求证:△ABE≌△DAF;
(2)若AF=1,四边形ABED的面积为6,求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 的边长为8,点
的边长为8,点![]() 是
是![]() 的内心,
的内心,![]() ,绕点
,绕点![]() 旋转
旋转![]() ,分别交线段
,分别交线段![]() 、
、![]() 于
于![]() 、
、![]() 两点,连接
两点,连接![]() ,给出下列四个结论:①点
,给出下列四个结论:①点![]() 也一定是
也一定是![]() 的外心;②
的外心;②![]() ;③四边形
;③四边形![]() 的面积始终等于
的面积始终等于![]() ;④
;④![]() 周长的最小值为6.上述结论中正确的个数是( )
周长的最小值为6.上述结论中正确的个数是( )
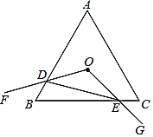
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为落实教育局“教育信息化2.0行动计划”,搭建数字化校园平台,需要购买一批电子白板和平板电脑,若购买2台电子白板和6台平板电脑共需9万元;购买3台电子白板和4台平板电脑共需11万元.
(1)求电子白板和平板电脑的单价各是多少万元?
(2)结合学校实际,该校准备购买电子白板和平板电脑共100台,其中电子白板至少购买6台且不超过24台,某商家给出了两种优惠方案,方案一:电子白板和平板电脑均打九折;方案二:买1台电子白板,送1台平板电脑.若购买电子白板a(台)所需的费用为W(万元),请根据两种优惠方案分别写出W关于a的函数关系式,并分析该校应选用哪种优惠方案购买更省钱.
查看答案和解析>>
科目:初中数学 来源: 题型:
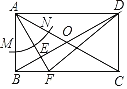
【题目】如图,在矩形ABCD中,对角线AC与BD交于点O,已知AB=OA,按以下步骤作图:①以点A为圆心,以任意长为半径画弧交AB于M,交AC于点N;②分别以点M,N为圆心,以大于![]() MN为半径画弧,两弧相交于点E;③作射线AE交BC于点F,连接DF.若AB=
MN为半径画弧,两弧相交于点E;③作射线AE交BC于点F,连接DF.若AB=![]() ,则线段DF的长为_____.
,则线段DF的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com