
����Ŀ��������������ֵ��֪ʶ�ش��������⣺
��1����ʾ��3��2����֮��ľ�����_____��һ��أ������ϱ�ʾ��m����n������֮��ľ������|m��n|��
���|a+2|��3����ôa��_____��
��2���������ϱ�ʾ��a�ĵ�λ�ک�4��2֮�䣬��|a+4|+|a��2|��ֵΪ_____��
��3�����������ҳ����з���������������x��ʹ��|x+2|+|x��5|��7����Щ���ʾ�����ĺ���_____��
��4����a��_____ʱ��|a+3|+|a��1|+|a��4|��ֵ��С����Сֵ��_____��
![]()
���𰸡�5 ��5��1 6 12 1 7
��������
(1)����������ľ���ֱ���ô�����ȥС�����ɵõ���|a+2|���Ի�Ϊ|a-(-2)|��|2-(-a)|���ټ���õ����.
(2) ��Ϊx�����˷�Χ,��a+4��0��a-2��0���ٸ��������ľ���ֵ���������������ľ���ֵ�������෴���Ĺ���ȥ����.Ȼ����м��㼴�ɵý⣻
(3) |x+2|�ɻ�Ϊ|x-(-2)|�����ʾ��x����-2��ͬ��|x��5|��ʾ��x����5�ľ��룬���xֻ���ǩ�2��5֮��������㣬������Щ����������Ӽ�����⣻
(4) ͨ�����Ϸ�����֪|a+3|+|a��1|+|a��4|��ʾ��a�ֱ����-3��1��4�ľ���͵���Сֵ.�жϳ�a��1ʱ����������ֵ�ĺ���С��Ȼ����м��㼴�ɵý⣮
�⣺��1��|2������3��|��5��
��|a+2|��3��
��a+2����3��a+2��3��
���a����5��a��1��
��2���߱�ʾ��a�ĵ�λ�ک�4��2֮�䣬
��a+4��0��a��2��0��
��|a+4|+|a��2|����a+4��+[����a��2��]��a+4��a+2��6��
��3��ʹ��|x+2|+|x��5|��7���������Щ�2����1��0��1��2��3��4��5��
��2��1+0+1+2+3+4+5��12��
����Щ���ʾ�����ĺ���12��
��4��
|a+3|+|a��1|+|a��4|��ʾ��a�ֱ����-3��1��4�ľ����
��a��-3��4֮���1��ʱ����a��1����Сֵ����Сֵ��|1+3|+|1��1|+|1��4|��4+0+3��7��
�ʴ�Ϊ��5����5��1��6��12��1��7��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ѧУ��Ҫ���ý�ʦ�칫����A��B����200�ף���֪2��A�����κ�1��B�����ι���2000Ԫ��1��A�����κ�3��B�����ι���3000Ԫ��
��1����A��B�������εĵ��ۣ�
��2������ҪA�����β�����120�ף�B�����β�����70�ף�ƽ��ÿ��������Ҫ�˷�10Ԫ���蹺��A������x��ʱ���ܷ���ΪyԪ����y��x�ĺ�����ϵʽ����ֱ��д��x��ȡֵ��Χ��
��3������ܷ������ٵĹ��÷�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ���˽�ijУ���꼶���������������������ʦ�漴��ȡ�������������������ϲ��ԣ����Գɼ�������ͳ�ƣ����Ƴ�ͼ1��ͼ2�в�������ͳ��ͼ.
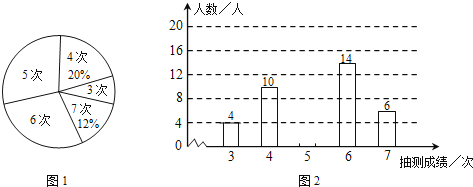
��1�����γ��������ж����ˣ�
��2�����㽫ͼ2��ͳ��ͼ����������
��3�����涨��������5�����ϣ���5�Σ�Ϊ���ܴ�꣬���У350�����꼶�����У������ж��������ܴ�ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
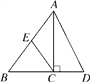
����Ŀ����ͼ���ڡ�ABD�У�AC��BD�ڵ�C�� ![]() ����E��AB���е㣬tanD��2��CE��1����sin��ECB��ֵ��AD�ij���
����E��AB���е㣬tanD��2��CE��1����sin��ECB��ֵ��AD�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������κ���y1��y2��ͼ��Ķ���ֱ�Ϊ��a��b������c��d������a=��c��b=2d���ҿ��ڷ�����ͬʱ�����y1��y2�������������κ�������
��1����д�����κ���y=x2+x+1��һ�������������κ�������
��2����֪����x�Ķ��κ���y1=x2+nx�Ͷ��κ���y2=nx2+x������y1+y2ǡ��y1��y2�������������κ���������n��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����A��B��C������ͬһֱ���ϣ����߶�AB=6 cm��BC=4 cm����M��N�ֱ�ΪAB��BC���е㣬��ôM��N����֮��ľ���Ϊ( )
A. 5 cm B. 1 cm C. 5��1 cm D. ��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������
(1)![]() (2)
(2)![]()
(3)��54��![]() ��
��![]() ��
��![]() (4)
(4)![]()
(5)��5��![]() +����9����
+����9����![]() +17��
+17��![]() (6)
(6)![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ����
����![]() �ش�;�绰����ʱ�շѣ�3�������շ�2.7Ԫ��3���Ӻ�ÿͨ��1�����շ�1.2Ԫ��ij����
�ش�;�绰����ʱ�շѣ�3�������շ�2.7Ԫ��3���Ӻ�ÿͨ��1�����շ�1.2Ԫ��ij����![]() ����
����![]() �ش�绰������
�ش�绰������![]() ����
����![]() Ϊ����)���ӣ�����Ϊ
Ϊ����)���ӣ�����Ϊ![]() Ԫ��
Ԫ��
(1)�![]() ��
��![]() ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
(2)��ͨ��5���ӣ�����Ҫ���Ѷ���Ԫ?
(3)��ij��ͨ������Ϊ8.7Ԫ������ͨ�����ٷ���?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��BC����ƽ��2cm�õ���DEF������ABC���ܳ�Ϊ16cm���t���x��ABFD���ܳ�Ϊ( )

A. 16cmB. 18cmC. 20cmD. 22cm
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com