
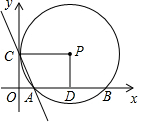
 如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点.若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6.
如图,以矩形OCPD的顶点O为原点,它的两条边所在的直线分别为x轴和y轴建立直角坐标系.以点P为圆心,PC为半径的⊙P与x轴的正半轴交于A、B两点.若抛物线y=ax2+bx+4经过A,B,C三点,且AB=6.分析 (1)根据垂径定理可得AD=DB=3,在Rt△PAD中,根据PA=$\sqrt{P{D}^{2}+A{D}^{2}}$即可解决问题.
(2)先确定A、B两点坐标,再根据待定系数法即可解决问题.
(3)根据对称性即可解决问题.
解答 解:(1)如图1中,连接PA.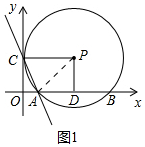
∵PD⊥AB,
∴AD=DB=$\frac{1}{2}$AB=3,
∵抛物线y=ax2+bx+4与y轴交于点C,
∴C(0,4),
∴OC=4,
∵四边形PDOC是矩形,
∴PD=OC=3,∠PDA=90°,
∴PC=PA=$\sqrt{P{D}^{2}+A{D}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴R=5.
(2)由(1)可知A(,2,0),B(8,0),
把A、B两点坐标代入y=ax2+bx+4得到,$\left\{\begin{array}{l}{4a+2b+4=0}\\{64a+8b+4=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=\frac{1}{4}}\\{b=-\frac{5}{2}}\end{array}\right.$,
∴抛物线的解析式为y=$\frac{1}{4}$x2-$\frac{5}{2}$x+4.
(3)如图2中,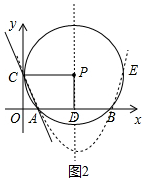
根据对称性,点C、点E关于对称轴x=5对称,
∵点C(0,4)
∴点E坐标(10,4).
点评 本题考查圆综合题、垂径定理、二次函数、待定系数法、矩形的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
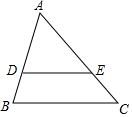 如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是( )
如图,在△ABC中,DE∥BC,$\frac{DE}{BC}$=$\frac{2}{3}$,△ADE的面积是8,则四边形DBCE的面积是( )| A. | 10 | B. | 18 | C. | 8 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
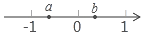 有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是( )
有理数a,b在数轴上对应的位置如图所示,那么代数式$\frac{|a+1|}{a+1}$-$\frac{|a|}{a}$+$\frac{b-a}{|a-b|}$-$\frac{1-b}{|b-1|}$的值是( )| A. | 2 | B. | 0 | C. | 1 | D. | -1 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
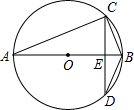 如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )
如图,AB是⊙O的直径,CD为弦,CD⊥AB于点E,则下列结论中不成立的是( )| A. | ∠A=∠D | B. | CE=DE | C. | CE=BD | D. | ∠ACB=90° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a+(b-c)=a+b+c | B. | a-(b-c)=a-b-c | C. | a-(-b+c)=a-b-c | D. | a-(-b-c)=a+b+c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
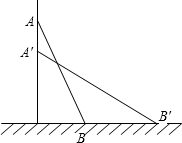 一架梯子长2.5米,斜靠在一面垂直于地面的墙上,梯子底端离墙0.7米.
一架梯子长2.5米,斜靠在一面垂直于地面的墙上,梯子底端离墙0.7米.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-3x+1=0 | B. | $\frac{1}{{x}^{2}}$=0 | C. | ax2+bx+c=0 | D. | x+3=4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com