
【题目】如图,正方形ABCD在平面直角坐标系中,且AD∥x轴,点A的坐标为(﹣4,1),点D的坐标为(0,1),点B,P都在反比例函数y= ![]() 的图象上,且P时动点,连接OP,CP.
的图象上,且P时动点,连接OP,CP. 
(1)求反比例函数y= ![]() 的函数表达式;
的函数表达式;
(2)当点P的纵坐标为 ![]() 时,判断△OCP的面积与正方形ABCD的面积的大小关系.
时,判断△OCP的面积与正方形ABCD的面积的大小关系.
【答案】
(1)解:∵四边形ABCD是正方形,A(﹣4,1),D(0,1),
∴OD=1,BC=DC=AD=4,
∴OC=3,
∴点B的坐标为(﹣4,﹣3).
∵点B在反比例函数y= ![]() 的图象上,
的图象上,
∴k=﹣4×(﹣3)=12,
∴反比例函数的表达式为y= ![]() ;
;
(2)解:∵点P在反比例函数y= ![]() 的图象上,点P的纵坐标为
的图象上,点P的纵坐标为 ![]() ,
,
∴点P的横坐标为 ![]() ,
,
∴S△OCP= ![]() ×3×
×3× ![]() =16.
=16.
∵S正方形ABCD=16,
∴△OCP的面积与正方形ABCD的面积相等.
【解析】(1)只需根据条件求出点B的坐标,然后运用待定系数法就可解决问题;(2)易求出OC的长,然后只需根据条件求出点P的横坐标,就可求出△OCP的面积,然后再求出正方形ABCD的面积,就可解决问题.


 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案科目:初中数学 来源: 题型:
【题目】二次函数y1=x2﹣2x﹣1与反比例函数y2=﹣ ![]() (x>0)的图象在如图所示的同一坐标系中,若y1>y2时,则x的取值范围( )
(x>0)的图象在如图所示的同一坐标系中,若y1>y2时,则x的取值范围( )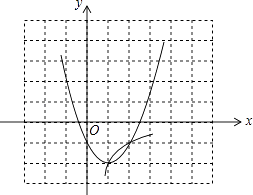
A.﹣1<x<1 或 x>2
B.1<x<2
C.x<1
D.0<x<1或x>2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为6的菱形ABCD中,∠DAB=60°,以点D为圆心,菱形的高DF为半径画弧,交AD于点E,交CD于点G,则图中阴影部分的面积是( )
A.18 ![]() ﹣9π
﹣9π
B.18﹣3π
C.9 ![]() ﹣
﹣ ![]()
D.18 ![]() ﹣3π
﹣3π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),
C(3,4)
⑴ 作出与△ABC关于y轴对称△A1B1C1,并写出 三个顶点的坐标为:A1( ),B1( ),C1( );
⑵ 在x轴上找一点P,使PA+PB的值最小,请直接写出点P的坐标;
⑶ 在 y 轴上是否存在点 Q,使得S△AOQ=![]() S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。
S△ABC,如果存在,求出点 Q 的坐标,如果不存在,说明理由。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算
(1)(3x-2y)2-2x(3x-2y);
(2)(2a+1)(4a2-2a+1);
(3)先化简,再求值:
(-x-2y)(x-2y)-(2y-x)2+(2x3-4x2y)÷2x,其 中x=-3,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,线段AB和射线BM交于点B.
(1)利用尺规完成以下作图,并保留作图痕迹(不写作法)
①在射线BM上作一点C,使AC=AB;
②作∠ABM 的角平分线交AC于D点;
③在射线CM上作一点E,使CE=CD,连接DE.
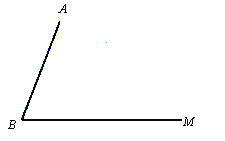
(2)在(1)所作的图形中,猜想线段BD与DE的数量关系,并证明之.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在日常生活中,如取款、上网等都需要密码.有一种用“因式分解”法产生的密码,方便记忆.原理是:如对于多项式x4-y4,因式分解的结果是(x-y)(x+y)·(x2+y2),若取x=9,y=9时,则各个因式的值是:(x-y)=0,(x+y)=18,x2+y2=162,于是就可以把“018162”作为一个六位数的密码.对于多项式4x3-xy2,取x=10,y=10时,用上述方法产生的密码共有多少种?请你分别写出来.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com