练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABE中，∠BAE＝105°，AE的垂直平分线MN交BE于点C，且AB＝CE，则∠B的度数是(　　)

    A. 45°B. 60°C. 50°D. 55°

    【答案】C

    【解析】

    已知MN是AE的垂直平分线，根据线段垂直平分线的性质可得AC=EC，所以∠CAE=∠E，由三角形外角的性质可得∠ACB=∠CAE+∠E=2∠E，再根据等腰三角形的性质可得∠B=∠ACB=2∠E，在△ABC中，根据三角形的内角和定理求得∠E=25°，即可求得∠B=2∠E=50°.

    ∵MN是AE的垂直平分线，

    ∴AC=EC，

    ∴∠CAE=∠E，

    ∴∠ACB=∠CAE+∠E=2∠E，

    ∵AB＝CE，

    ∴∠B=∠ACB=2∠E，

    在△ABC中，∠BAE+∠B+∠E=180°，

    ∴105°+2∠E+∠E=180°

    即∠E=25°.

    ∴∠B=2∠E=50°.

    故选C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某种型号汽车油箱容量为40L，每行驶100km耗油10L.设一辆加满油的该型号汽车行驶路程为x（km），行驶过程中油箱内剩余油量为y（L）

    （1）求y与x之间的函数表达式；

    （2）为了有效延长汽车使用寿命，厂家建议每次加油时油箱内剩余油量不低于油箱容量的四分之一，按此建议，求该辆汽车最多行驶的路程.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在东营市中小学标准化建设工程中，某学校计划购进一批电脑和电子白板，经过市场考察得知，购买1台电脑和2台电子白板需要3.5万元，购买2台电脑和1台电子白板需要2.5万元.

    （1）求每台电脑、每台电子白板各多少万元?

    （2）根据学校实际，需购进电脑和电子白板共30台，总费用不超过30万元，但不低于28万元，请你通过计算求出有几种购买方案，哪种方案费用最低.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】发现（1）如图1，把△ABC沿DE折叠，使点A落在点A’处，请你判断∠1+∠2与∠A有何数量关系，直接写出你的结论，不必说明理由

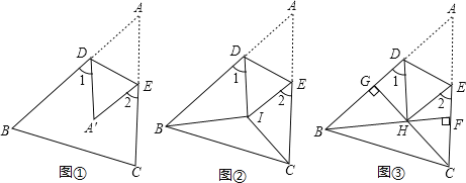
    思考（2）如图2，BI平分∠ABC，CI平分∠ACB，把△ABC折叠，使点A与点I重合，若∠1+∠2=100°，求∠BIC的度数；

    拓展（3）如图3，在锐角△ABC中，BF⊥AC于点F，CG⊥AB于点G，BF、CG交于点H，把△ABC折叠使点A和点H重合，试探索∠BHC与∠1+∠2的关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在四边形ABCD中，∠A=∠C=90°，∠B=α，在AB，BC上分别找一点E,F,使△DEF的周长最小，此时，∠EDF=______。（用含α的代数式表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠AGF=∠ABC，∠1+∠2=180°．

    (1)试判断BF与DE的位置关系，并说明理由；

    (2)若BF⊥AC，∠2=150°，求∠AFG的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD是线段AB的垂直平分线，则∠CAD=∠CBD.请说明理由：

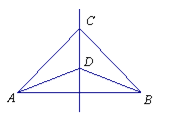
    解：∵ CD是线段AB的垂直平分线

    ∴ AC=BC,AD=DB（ ）

    在△ADC和△BDC中，

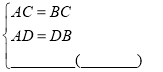
    ∴△ADC≌和△BDC( ）.

    ∴ ∠CAD=∠CBD（ ）.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知关于x的方程2（x+1）﹣m=﹣的解比方程5（x﹣1）﹣1=4（x﹣1）+1的解大2．

    （1）求第二个方程的解；

    （2）求m的值．

    查看答案和解析>>

    同步练习册答案