
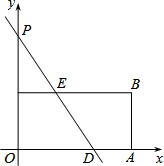
 ��ͼ����ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ���A��B������ֱ�Ϊ��12��0������12��6����ֱ��y=-$\frac{3}{2}$x+b��y�ύ�ڵ�P�����OA���ڵ�D�����BC���ڵ�E��
��ͼ����ƽ��ֱ������ϵ�У��ı���OABCΪ���Σ���A��B������ֱ�Ϊ��12��0������12��6����ֱ��y=-$\frac{3}{2}$x+b��y�ύ�ڵ�P�����OA���ڵ�D�����BC���ڵ�E������ ��1������ֱ��ƽ�־��ε�������ɵ�ֱ�߾����Խ��ߵ��е㣬���ݴ���ϵ�������ɵ�bֵ��
��2�����ݽ�ƽ���ߵ����ʣ��ɵá�1���2�Ĺ�ϵ������ƽ���ߵ����ʣ��ɵá�1���3�����ݵ��������ε��ж����ɵ�OM��MN�Ĺ�ϵ�����ݽⷽ�̣��ɵ�M�����ꣻ�����Ա����뺯��ֵ�Ĺ�ϵ���ɵ�D�����꣬�����߶εĺͲ�ɵô𰸣�
��� �⣺��1����ͼ1��
ֱ��y=-$\frac{3}{2}$x+bƽ�־���OABC���������
ֱ��y=-$\frac{3}{2}$x+b����OB���е�F��6��3����
��F��������뺯������ʽ����-$\frac{3}{2}$��6+b=3��
���b=12��
��2������ONƽ�֡�CNM��
��ͼ2�� ��
��
��ONƽ�֡�CNM��
���1=��2��
��OA��BC���á�1=��3��
���2=��3��
��OM=MN��
����ת���ֱ�߽���ʽΪy=kx+12��
��y=0ʱ��kx+12=0�����x=-$\frac{12}{k}$����M��-$\frac{12}{k}$��0����
��y=6ʱ��kx+12=6�����x=-$\frac{6}{k}$����N��-$\frac{6}{k}$��6����
��OM=MN����OM2=MN2������-$\frac{12}{k}$��2=��-$\frac{12}{k}$+$\frac{6}{k}$��2+62��
���k=-$\sqrt{3}$��k=$\sqrt{3}$�����������⣬�ᣩ
OM�ij�ΪM��ĺ����꣬-$\frac{12}{k}$=-$\frac{12}{-\sqrt{3}}$=4$\sqrt{3}$����M��4$\sqrt{3}$��0����
y=-$\frac{3}{2}$x+12��x��Ľ���ΪD��
��y=0ʱ��-$\frac{3}{2}$x+12=0�����x=8����D��8��0����
MD=8-4$\sqrt{3}$��
���� ���⿼����һ�κ����ۺ��⣬��1������ֱ��ƽ�־��ε�����ó�ֱ�߾������ζԽ��ߵ��е��ǽ���ؼ�����2�����õ��������ε��ж��ó�OM=MN�ǽ���ؼ������������Ա����뺯��ֵ�Ķ�Ӧ��ϵ��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
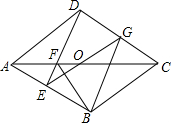 ��֪����ͼ��������ABCD�У�E��AB��һ�㣬�߶�DE�����ζԽ���AC���ڵ�F����O��AC���е㣬EO���ӳ��߽���DC�ڵ�G
��֪����ͼ��������ABCD�У�E��AB��һ�㣬�߶�DE�����ζԽ���AC���ڵ�F����O��AC���е㣬EO���ӳ��߽���DC�ڵ�G�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
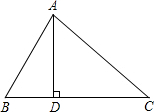 ��֪����ͼ���ڡ�ABC�У�AD��BC��D����B=60�㣬��C=45�㣮
��֪����ͼ���ڡ�ABC�У�AD��BC��D����B=60�㣬��C=45�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 6 | B�� | -3 | C�� | 1 | D�� | 3 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com