
����Ŀ����ͼ������������y��![]() ��x��0����һ�κ���y��mx+n��ͼ�����㣨�����ߵĽ��㣩B��P��
��x��0����һ�κ���y��mx+n��ͼ�����㣨�����ߵĽ��㣩B��P��

��1������������һ�κ����Ľ���ʽ��
��2���۲�ͼ��ֱ��д��һ�κ���ֵ���ڷ���������ֵʱx��ȡֵ��Χ�ǣ��� ����
��3����ͼ����ֱ�ߺ�2BǦ�ʻ����������Σ���д��������Ҫ��ÿ�����ξ���������������������
���ĸ�������ڸ���ϣ���������������ֱ��ǵ�O����P��
�ھ��ε��������k��ֵ��
���𰸡���1��y��![]() ��y����
��y����![]() +3����2��2��x��4����3��������
+3����2��2��x��4����3��������
��������
��1�����ô���ϵ�����������������������һ�κ����Ľ���ʽ��
��2������ͼ����ã�
��3�����ݾ������������������������Ҫ����������μ��ɣ�
��1���߷���������y��![]() ��x��0����ͼ������P��2��2����
��x��0����ͼ������P��2��2����
��k��2��2��4��
�෴���������Ľ���ʽΪy��![]() ��
��
��һ�κ���y��mx+n��ͼ������P��2��2����B��4��1����
��![]() �����
����� ��
��
��һ�κ����Ľ���ʽΪy����![]() +3��
+3��
��2��һ�κ���ֵ���ڷ���������ֵʱx��ȡֵ��Χ��2��x��4��
�ʴ�Ϊ2��x��4��
��3����ͼ��ʾ��
����OAPE������ODFP��Ϊ��������ͼ�Σ�



 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�����������ڽǻ�����ı��γ�Ϊ�����ı��Σ��������ǵļб߳�Ϊ�����ߣ�
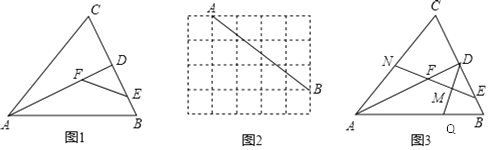
��1����ͼ1������ABC�У�AB=AC��AD����ABC�Ľ�ƽ���ߣ�E��F�ֱ���BD��AD�ϵĵ㣮��֤���ı���ABEF�������ı��Σ�
��2����ͼ2����5��4�ķ���ֽ�У�A��B�ڸ���ϣ��뻭��һ�����������������ı���ABEF��ʹAB�������ߣ�E��F�ڸ���ϣ�
��3����ͼ3���ڣ�1���������£�ȡEF�е�M������DM���ӳ���AB�ڵ�Q���ӳ�EF��AC�ڵ�N����NΪAC���е㣬DE=2BE��QB=6����������AB�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
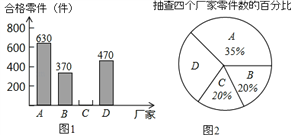
����Ŀ��Ϊ��Ӧ���ҵġ�һ��һ·�����÷�չս�ԣ�����Ʒ����ʶ�������ʼ첿�Ŷ�A��B��C��D�ĸ�����������ͬ���ͺŵ������2000�����кϸ��ʼ�⣬ͨ�����ó�C���ҵĺϸ���Ϊ95%�������ݼ�����ݻ�������ͼ1��ͼ2������������ͳ��ͼ��
��1�����D���ҵ����Ϊ�� ����������ͳ��ͼ��D���Ҷ�Ӧ��Բ�Ľ�Ϊ�� ����
��2�����C���ҵĺϸ����Ϊ�� ����������ͼ1����������
��3��ͨ������˵���ϸ�������ǰ�����������������ң�
��4����Ҫ��A��B��C��D�ĸ������У������ȡ�������Ҳμӵ¹���ҵ��Ʒ�����ᣬ���á��б�����������ͼ���ķ��������3������������ͬʱ��ѡ�еĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��С����AB����С����CD����С�죨EF��ͬʱվ��·���µı�ֱ·���ϣ�����С����С���Ӱ�ӷֱ���BD��FM��

��1��������ͼ�л���·�Ƶ������ڵ�λ�ã��õ�P��ʾ����������С��AB��ʱ��·���µ�Ӱ�ӣ����߶�BN��ʾ����
��2����С����С�����߶���1.7�ף�С������1.8�ף�BD��2�ף�DF��3�ף�FM��1�ף���·�Ƹ߶Ⱥ�С��Ӱ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ں�����һ��С����С����֪�������ĸ����ĸ߶ȣ��������ڰ������˲���ǣ����������������£���ͼ��ʾ����������λ��![]() ��ˮƽ��
��ˮƽ��![]() �ľ���Ϊ1.5�ף���
�ľ���Ϊ1.5�ף���![]() �����������
�����������![]() ������Ϊ
������Ϊ![]() ������
������![]() �������������ˮ�е�Ӱ
�������������ˮ�е�Ӱ![]() ����
����![]() ���ĸ���Ϊ
���ĸ���Ϊ![]() ���������������������������ĸ߶ȣ���
���������������������������ĸ߶ȣ���![]() ��.
��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У���8�������Ϊ1��С��������ɵ�L��ģ����ͼ���ã������ABCD���ܳ�Ϊ��������

A.12![]() B.10
B.10![]() C.8
C.8![]() D.8+4
D.8+4![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����OABC���Ե�OΪ����ԭ�㽨��ƽ��ֱ������ϵ������A��2��0����C��0��3������P��ÿ��1����λ���ٶȴӵ�C����������CO���˶�������BP����BE��PB��x���ڵ�E������PE��AB�ڵ�F�����˶�ʱ��Ϊt�룮
��1����t��4ʱ�����E�����ꣻ
��2�����˶��Ĺ����У��Ƿ������P��O��EΪ��������������ABE���ƣ������ڣ��������P�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ۺ���̽����
��ͼ����������![]() ����ƽ��
����ƽ��![]() ����λ���ȣ�������ƽ��
����λ���ȣ�������ƽ��![]() ����λ���Ⱥõ���������
����λ���Ⱥõ���������![]() ��ƽ�ƺ��������
��ƽ�ƺ��������![]() ��
��![]() ��ֱ���
��ֱ���![]() ,
,![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() .������
.������![]() �ĶԳ���
�ĶԳ���![]() ��������
��������![]() ���ڵ�
���ڵ�![]() .
.

��1������ֱ��д��������![]() �Ľ���ʽ����д������ʽ���ɣ�
�Ľ���ʽ����д������ʽ���ɣ�
��2�����![]() ,
,![]() ,
,![]() ��������ꣻ
��������ꣻ
��3����![]() ���ϴ���һ��
���ϴ���һ��![]() ��ʹ
��ʹ![]() ��ֵ��С�����
��ֵ��С�����![]() ������.
������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������˼������ͼ�١�ACB����ADB��90����ô��D�ھ���A��B��C�����Բ�ϣ���ͼ�ڣ������ACB����ADB����������90��������C��D��AB��ͬ�ࣩ����ô��D���ھ���A��B��C�����Բ�ϣ�

��Ӧ�ã����ı���ABCD�У�AD��BC����CAD��90������E�ڱ�AB�ϣ�CE��DE��
��1������ADF����AED����CA���ӳ����ڵ�F����ͼ�ܣ�����֤��DFΪRt��ACD�����Բ�����ߣ�
��2����ͼ�ݣ���G��BC���ӳ����ϣ���BGE����BAC����֪sin��AED��![]() ��AD��1����DG�ij���
��AD��1����DG�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com