
����Ŀ���ƴ���ʫ�����ϲ��������ʫ������С������ʫ��ƪ��֮˵�����㷨ͳ�ڡ��м�����һ��������ơ��Ĺ��£�ʫ�ƣ� ��Яһ���ƣ��δ������ߣ������һ����������붷����������꣬�������оƣ���������ʿ�����֪ԭ�У�
ע���Ŵ�һ����10����
�����ǣ�����ڽ��ⴺ��ʱ����������һ��Լ�����������ѣ��ȵ��Ƶ��ォ����ľ�����һ�����ٺȵ����е�5���ƣ�����������Լ�����ڵ�3�����������������úȹ��˺��еľƣ�
��1���з��������ԭ�ж������ƣ�
��2�������ԭ��a0���ƣ��ڵ�n�������ƺ������an���ƣ����һ�����������Ϊa1=2a0��5���������ڶ������������Ϊa2=2a1��5=22a0����22��1����5���������� �ú�an��1��ʽ�ӱ�ʾan= �� ���ú�a0��n��ʽ�ӱ�ʾan=��
��3���������Լ��������ڵ�4����ȹ��˺��оƣ���������еĽ��������ԭ�ж������ƣ�
���𰸡�
��1���⣺�����ԭ��x���ƣ�
��������ã�2[2��2x��5����5]=5��
��ã�x= ![]() ��
��
�𣺺���ԭ�� ![]() ����
����
��2��2an��1��5��2na0����2n��1����5
��3���⣺������ã�a4=24a0����24��1����5=16a0��75=0��
��ã�a0= ![]() ��
��
������ڵ�4����ȹ��˺��оƣ������ԭ�� ![]() ����
����
������������������⣺ ��2���ٹ۲죬���֣�a1=2a0��5��a2=2a1��5=22a0����22��1����5��a2=2a1��5=22a0����22��1����5��a3=2a2��5=23a0����23��1����5������ ��an=2an��1��5=2na0����2n��1����5��
�ʴ�Ϊ��2an��1��5��2na0����2n��1����5��
��1�������ԭ��x���ƣ����ڵ�3�����������������úȹ��˺��еľƿɵó�����x��һԪһ�η��̣���֮���ɵó����ۣ���2������a1��a2��a3�ı仯���ҳ��仯���ɡ�an=2an��1��5=2na0����2n��1����5��������ý⣻��3����an=2an��1��5=2na0����2n��1����5��n=4��an=0���ɵó�����a0��һԪһ�η��̣���֮���ɵó����ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���չ�������5000Ԫ����һ����Ʒ�ֵ�ƻ��������������������״�����ã������ֵ���11000Ԫ�ʽ�����ƻ��������εĽ��۱�����ʱÿǧ�˶���0.5Ԫ������ƻ��������������ʱ��2����
��1������ʱ��Ʒ��ƻ���Ľ�����ÿǧ�˶���Ԫ��
��2��������н���Ʒ�ֵ�ƻ����ÿǧ��7Ԫ���۳��ۣ�����ƻ���۳������µ�400ǧ�������۵��������꣬��ô������������ƻ�������й�ӯ������Ԫ����7�֣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����x2+x��3��0�������ʽ2��x��2����x+2����x��x��1����ֵ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ���д�����ǣ� ��.
A.-3.14��-��
B.3.5��-4
C.-17/3��-23/4
D.-0.21��-0.21
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı�������E�DZ�CD��һ������BC��EC��CF��BE��AB�ڵ�F��P��EB�ӳ�����һ�������н��ۣ���BEƽ����CBF����CFƽ����DCB����BC��FB����PF��PC��������ȷ���۵ĸ���Ϊ( )
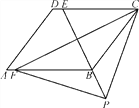
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ϣ���A��ʾ��a������A����ƽ��4����λ���ȵõ���B����B��ʾ��b����|a|��|b|����a��ֵΪ��������
A.��3B.��2C.��1D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��0Ϊԭ�㣬A��4��0����E��0��3�����ı���OABC���ı���OCDE��Ϊƽ���ı��Σ�OC=5������y=![]() ��x��0����ͼ��AB���е�F��DE���е�G����k��ֵΪ ��
��x��0����ͼ��AB���е�F��DE���е�G����k��ֵΪ ��
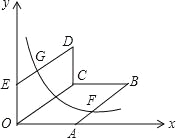
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ı���ABCD�������Σ���ʾ���������ı���ȣ��ĸ��Ƕ���90����
��ͼ1����G��BC��������һ��(�����B��C�غ�)������AG����BF��AG�ڵ�F��
DE��AG�ڵ�E����֤����ABF�ա�DAE��
(2) ����ͼ2������G��CD��������һ��(�����C��D�غ�)������AG����BF��AG�ڵ�F��
DE��AG�ڵ�E���߶�EF��AF��BF�ĵ�����ϵ��______ ___��
����ͼ3������G��CD�ӳ���������һ�㣬����AG����BF��AG�ڵ�F��DE��AG�ڵ�E��
�߶�EF��AF��BF�ĵ�����ϵ��______ ��
(3)����G��BC�ӳ���������һ�㣬����AG����BF��AG�ڵ�F��DE��AG�ڵ�E���뻭ͼ��
̽���߶�EF��AF��BF�ĵ�����ϵ��
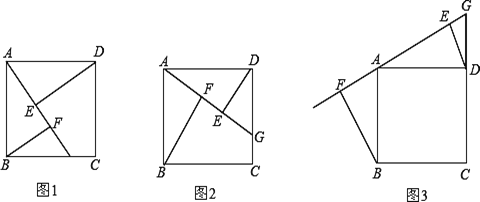
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com