练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    3．如图，⊙O的半径为4，PC切⊙O于点C，交直径AB延长线于点P，若CP长为4，则阴影部分的面积为8-2π．

    分析 利用切线的性质结合等腰直角三角形的性质得出∠COP=∠CPO=45°，进而利用阴影部分的面积为：S△COP-S扇形COB求出即可．

    解答 解：连接CO，
    ∵PC切⊙O于点C，
    ∴OC⊥PC，
    ∵⊙O的半径为4，CP长为4，
    ∴CO=CP，
    ∴∠COP=∠CPO=45°，
    ∴阴影部分的面积为：S△COP-S扇形COB=$\frac{1}{2}$×4×4-$\frac{45π×{4}^{2}}{360}$=8-2π．
    故答案为：8-2π．

    点评 此题主要考查了切线的性质以及扇形面积公式等知识，得出∠COP=∠CPO=45°是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    13．如果点A（-2，y1），B（-1，y2），C（2，y3）都在反比例函数y=$\frac{{k}^{2}+1}{x}$的图象上，那么y1、y2、y3的大小关系是y3＞y1＞y2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

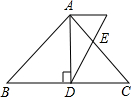    14．如图，AD是等腰△ABC底边上的高，且AD=4，sinB=$\frac{4}{5}$，若E是AC边上的点，且满足AE：EC=2：3，连接DE，求cot∠ADE的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    11．数学活动课上，小敏、小颖分别画了△ABC和△DEF，尺寸如图．如果两个三角形的面积分别记作S△ABC、S△DEF，那么它们的大小关系是（　　）
    A．S△ABC＞S△DEFB．S△ABC＜S△DEFC．S△ABC=S△DEFD．不能确定

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18． 某学校准备组织八年级学生春游，供学生选择的春游地点分别是：植物园、太阳岛、东北虎林园．每名学生只能选择其中一个春游地点（必选且只选一个）．该校从八年级学生中随机抽取了a名学生，对他们选择春游地点的情况进行调查，并根据调查结果绘制成如图所示的条形统计图．
    （1）求a的值；
    （2）求a名学生中选择去植物园春游的人数占所抽取人数的百分比是多少？
    （3）如果该校八年级有440名学生，请你估计选择去太阳岛春游的学生有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，AB为⊙O的弦，△ABC的两边BC、AC分别交⊙O于D、E两点，其中∠B=60°，∠EDC=70°，则∠C=50度．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．定义一种运算：${a_k}={a_{k-1}}+1-5（{[{\frac{k-1}{5}}]-[{\frac{k-2}{5}}]}）$，其中k是正整数，且k≥2，[x]表示非负实数x的整数部分，例如[2.6]=2，[0.8]=0．若a1=1，则a2014的值为4．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．在一个不透明的盒子里，装有5个黑球和若干个白球，这些球除颜色外都相同，将其摇匀后从中随机摸出一个球，记下颜色后再把它放回盒子中，不断重复，共摸球40次，其中10次摸到黑球，请估计盒子中白球的个数是（　　）
    A．10个B．15个C．20个D．25个

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．如图，△ABC是直角三角形，∠ACB=90°．
    （1）动手操作：利用尺规作∠ABC的平分线，交AC于点O，再以O为圆心，OC的长为半径作⊙O（保留作图痕迹，不写作法）；
    （2）综合运用：在你所作的图中，
    ①判断AB与⊙O的位置关系，并证明你的结论；
    ②若AC=12，tan∠OBC=$\frac{2}{3}$，求⊙O的半径．

    查看答案和解析>>

    同步练习册答案