
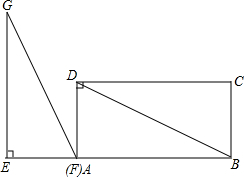
 如图,在矩形ABCD中,DB=6,AD=3,在Rt△EFG中,∠GEF=90°,EF=3,GF=6,△EFG(点F和点A重合)的边EF和矩形的边AB在同一直线上.现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,解答下列问题:
如图,在矩形ABCD中,DB=6,AD=3,在Rt△EFG中,∠GEF=90°,EF=3,GF=6,△EFG(点F和点A重合)的边EF和矩形的边AB在同一直线上.现Rt△EFG将从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,解答下列问题:分析 (1)当GF经过点D时,GE∥DA,由EF=3,GF=6,可得∠EGF=∠ADF=30°,用三角函数计算可得AF=$\sqrt{3}$,所以t=$\sqrt{3}$.
(2)根据题意,分三种情况讨论:①当0≤t<$\sqrt{3}$时,②当$\sqrt{3}$≤t<3时,③当3≤t≤6时,根据三角形、梯形的面积的求法,求出S与t的函数关系式即可.
(3)根据题意,分三种情况讨论:①当DM=DN时;②当DN=MN时;③当DM=MN时;然后根据等腰三角形的性质,分类讨论,求出α的值以及DM的长度各是多少即可.
解答 解:在Rt△ABD中,∠DAB=90°,DB=6,AD=3,
∴∠DBA=30°,∠ADB=60°,AB=DB•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$,
在Rt△GEF中,∠GEF=90°,EF=3,GF=6,
∴∠EGF=30°,∠EFG=60°,GE=GF•cos30°=6×$\frac{\sqrt{3}}{2}$=3$\sqrt{3}$.
(1)如图1,当GF经过点D时,GE∥DA, ,
,
∵EF=3,GF=6,
∴∠EGF=∠ADF=30°,
又∵AD=3,
∴AF=tan30°×AD=$\frac{\sqrt{3}}{3}$×3=$\sqrt{3}$,
∴当△EFG运动到$\sqrt{3}$秒时,GF经过点D.
(2)①如图2,当0≤t<$\sqrt{3}$时, ,
,
∵AF=t,AH=$\sqrt{3}$t,
∴S=$\frac{1}{2}$×t×$\sqrt{3}$t,
=$\frac{\sqrt{3}}{2}$t2.
②如图3,当$\sqrt{3}$≤t<3时,作PQ⊥AB于点Q, ,
,
∵AF=t,
∴BF=3$\sqrt{3}$-t,
∵BQ=$\sqrt{3}$PQ,QF=$\frac{\sqrt{3}}{3}$PQ,
∴QF=$\frac{1}{3}$BQ,QF=$\frac{3\sqrt{3}-t}{2}$,
∴PQ=$\sqrt{3}$QF=$\frac{9-\sqrt{3}t}{2}$,
∴S=S△BAD-S△BFP=$\frac{1}{2}$×3×3$\sqrt{3}$-$\frac{1}{2}$×(3$\sqrt{3}$-t)×$\frac{9-\sqrt{3}t}{2}$=-$\frac{\sqrt{3}}{4}$t2+$\frac{9}{2}$t-$\frac{9\sqrt{3}}{4}$.
③如图4,当3≤t≤6时,GE与BD交于点M, ,
,
BE=3$\sqrt{3}$-(t-3)=3$\sqrt{3}$+3-t,EM=$\frac{\sqrt{3}}{3}$BE=3+$\sqrt{3}$-$\frac{\sqrt{3}}{3}t$,BF=3$\sqrt{3}$-t,PQ=$\frac{9-\sqrt{3}t}{2}$,
∴S=S△BEM-S△BFP=$\frac{1}{2}$×(3$\sqrt{3}$+3-t)×(3+$\sqrt{3}$-$\frac{\sqrt{3}}{3}t$)-$\frac{1}{2}$×(3$\sqrt{3}$-t)×$\frac{9-\sqrt{3}t}{2}$=-$\frac{\sqrt{3}}{12}$t2+$\frac{3-2\sqrt{3}}{2}$t$+9-\frac{3\sqrt{3}}{4}$.
综上,可得
S=$\left\{\begin{array}{l}{{\frac{\sqrt{3}}{2}t}^{2},0≤t<\sqrt{3}}\\{-{\frac{\sqrt{3}}{4}t}^{2}+\frac{9}{2}t-\frac{9\sqrt{3}}{4},\sqrt{3}≤t<3}\\{-{\frac{\sqrt{3}}{12}t}^{2}+\frac{3-2\sqrt{3}}{2}t+9-\frac{3\sqrt{3}}{4},3≤t≤6}\end{array}\right.$
(3)存在α,使△DNM为等腰三角形.
①如图5,当DM=DN时, ,
,
∵DM=DN,
∴∠DMN=∠DNM=(180°-∠MDN)÷2=(180°-30°)÷2=75°,
∵∠BNE=∠DNM=75°,
∴∠NBE=90°-∠BNE=90°-75°=15°,
∴α=∠ABD-∠NBE=30°-15°=15°,
∴BN=$\frac{BE}{sin75°}$=$\frac{3}{sin(45°+30°)}$=$\frac{3}{\frac{\sqrt{6}+\sqrt{2}}{4}}$=3$\sqrt{6}$-3$\sqrt{2}$,
∴DM=DN=DB-BN=6-(3$\sqrt{6}$-3$\sqrt{2}$)=6+3$\sqrt{2}$-3$\sqrt{6}$.
②如图6,当DN=MN时, ,
,
∵DN=MN,
∴∠MDN=∠DMN=30°,
∵∠DNM=180°-30°-30°=120°,
∴∠BNM=180°-∠DNM=180°-120°=60°,
∴∠EBN=90°-∠BNM=90°-60°=30°,
∴α=∠ABD+∠NBE=30°+30°=60°,
∴BN=$\frac{BE}{cos30°}$=$\frac{3}{\frac{\sqrt{3}}{2}}$=2$\sqrt{3}$,
∴MN=DN=DB-BN=6-2$\sqrt{3}$,
∴DM=2DH=2DN×cos30°=2×(6-2$\sqrt{3}$)×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}-6$.
③如图7,当DM=MN时,D、B、G三点共线,连接BM, ,
,
∵GBE=60°,
∴α=∠ABD+180°-∠GBE=30°+180°-60°=150°,
∵DM=MN,DB=GB,
∴MB⊥DG,
在Rt△MBG中,
∴DM=MN=$\frac{GB}{cos30°}=\frac{6}{\frac{\sqrt{3}}{2}}=4\sqrt{3}$.
综上,可得存在α,使△DNM为等腰三角形.
①当DM=DN时,α=15°,DM=6+3$\sqrt{2}$-3$\sqrt{6}$.
②当DN=MN时,α=60°,DM=6$\sqrt{3}$-6.
③当DM=MN时,α=150°,DM=4$\sqrt{3}$.
故答案为:$\sqrt{3}$.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,要熟练掌握.
(2)此题还考查了等腰三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:①等腰三角形的两腰相等.②等腰三角形的两个底角相等.③等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合.
(3)此题还考查了图形的平移,三角形的面积公式的运用,梯形的面积公式的运用,分段函数的解法的运用,三角函数值的运用,勾股定理的运用,等腰直角三角形的性质的运用,解答时寻找分段函数的分段点是难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
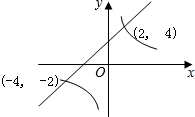 如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交点坐标为(2,4)、(-4,-2),点(a1,b)(a2,b)分别为一次函数和反比例函数图象上的一点,且a1>a2,则b的取值范围是-2<b<0,或b>4.
如图,已知一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交点坐标为(2,4)、(-4,-2),点(a1,b)(a2,b)分别为一次函数和反比例函数图象上的一点,且a1>a2,则b的取值范围是-2<b<0,或b>4.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com