
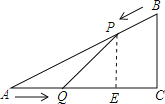
【题目】如图,在Rt△ABC中,AB=10cm,sinA=![]() .如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)
.如果点P由B出发沿BA向点A匀速运动,同时点Q由A出发沿AC向点C匀速运动.已知点P的速度为2cm/s,点Q的速度为1cm/s.连接PQ,设运动的时间为t(单位:s)(0≤t≤5)

(1)求AC,BC的长;
(2)当t为何值时,△APQ的面积为△ABC面积的![]() ;
;
(3)当t为何值时,△APQ与△ABC相似.
【答案】(1)AC=8cm,BC=6cm;(2)当t为1s或4s时,△APQ的面积为△ABC面积的![]() ;(3)当t为
;(3)当t为![]() s或
s或![]() s时,△APQ与△ABC相似.
s时,△APQ与△ABC相似.
【解析】
试题分析:(1)根据正弦的定义和勾股定理求出AC,BC的长;
(2)作PE⊥AC于E,根据相似三角形的性质用t表示出PE,根据三角形的面积公式和题意列出方程,解方程即可;
(3)分△APQ∽△ABC和△APQ∽△ACB两种情况,根据相似三角形的性质列出方程,解方程即可.
解:(1)∵Rt△ABC中,AB=10cm,sinA=![]() ,
,
∴![]() =
=![]() ,
,
∴BC=6cm,
则AC=![]() =8cm,
=8cm,
∴AC=8cm,BC=6cm;
(2)作PE⊥AC于E,
由题意得,BP=2tcm,AQ=tcm,
则AP=(10﹣2t)cm,
∵PE∥BC,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,PE=6﹣![]() t,
t,
∴△APQ的面积=![]() ×t×(6﹣
×t×(6﹣![]() t),△ABC面积=
t),△ABC面积=![]() ×6×8=24,
×6×8=24,
由题意得,![]() ×t×(6﹣
×t×(6﹣![]() t)=
t)=![]() ×24,
×24,
解得,t1=1,t2=4,
则当t为1s或4s时,△APQ的面积为△ABC面积的![]() ;
;
(3)当△APQ∽△ABC时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,t=![]() ,
,
当△APQ∽△ACB时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得,t=![]() ,
,
故当t为![]() s或
s或![]() s时,△APQ与△ABC相似.
s时,△APQ与△ABC相似.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连接AE、AF、EF.
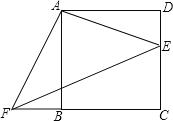
(1)求证:△ADE≌△ABF;
(2)填空:△ABF可以由△ADE绕旋转中心 点,按顺时针方向旋转 度得到;
(3)若BC=8,DE=6,求△AEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有2个白球,1个黑球和若干个红球,它们除颜色外其余都相同,从中任意摸出1个球,是白球的概率为![]() .
.
(1)布袋里红球有多少个?
(2)先从布袋中摸出1个球后不放回,再摸出1个球,请用列表或树状图灯方法求出两次摸到的球是1个红球和1个白球的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y=![]() 与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=
与一次函数y=k2x+b图象的交点为A(m,1),B(﹣2,n),OA与x轴正方向的夹角为α,且tanα=![]() .
.
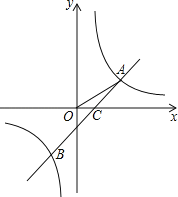
(1)求反比例函数及一次函数的表达式;
(2)设直线AB与x轴交于点C,且AC与x轴正方向的夹角为β,求tanβ的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
探究一:我们知道,三角形的一个外角等于与它不相邻的两个内角的和.那么,三角形的一个内角与它不相邻的两个外角的和之间存在何种数量关系呢?

已知:如图1,∠FDC与∠ECD分别为△ADC的两个外角,试探究∠A与∠FDC+∠ECD的数量关系.
探究二:三角形的一个内角与另两个内角的平分线所夹的钝角之间有何种关系?
已知:如图2,在△ADC中,DP、CP分别平分∠ADC和∠ACD,试探究∠P与∠A的数量关系.
探究三:若将△ADC改为任意四边形ABCD呢?
已知:如图3,在四边形ABCD中,DP、CP分别平分∠ADC和∠BCD,试利用上述结论探究∠P与∠A+∠B的数量关系.
探究四:若将上题中的四边形ABCD改为六边形ABCDEF(图4)呢?
请直接写出∠P与∠A+∠B+∠E+∠F的数量关系: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】扬州某楼盘准备以每平方米的10000元均价销售,经过两次下调后,决定以每平方米8600元的均价开盘.若设平均每次下调的百分率为x,则可列方程________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com