
【题目】如图,![]() 中,以
中,以![]() 为直径作⊙
为直径作⊙![]() ,交
,交![]() 于点
于点![]() ,
,![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 、
、![]() 、
、![]() ,交
,交![]() 于点
于点![]() .
.

(1)若![]() ,求证:
,求证:![]() 为⊙
为⊙![]() 的切线;
的切线;
(2)若![]() ,求证:
,求证:![]() 平分
平分![]() ;
;
(3)在(2)的条件下,若![]() ,求⊙
,求⊙![]() 的半径.
的半径.
【答案】(1)详见解析;(2)详见解析;(3)![]() .
.
【解析】
(1)根据AB为⊙![]() 直径,得出
直径,得出![]() =90°,即
=90°,即![]() °,
°,![]() ,
,![]() ,推出
,推出![]() ,即
,即![]() °,
°,
所以![]() =
=![]() =90°,得出AC为⊙
=90°,得出AC为⊙![]() 的切线;(2)证明
的切线;(2)证明![]() , 得到
, 得到![]() ,因为
,因为![]() ,所以
,所以![]() ,即可得到AE平分
,即可得到AE平分![]() ;(3)过点F作FH⊥AB于H可证
;(3)过点F作FH⊥AB于H可证![]() ,可得AH=AD=4,FH=DF=2;可证
,可得AH=AD=4,FH=DF=2;可证![]() 故
故![]() ;BH=x,则BD=2x,BF=2x-2,利用勾股定理可得
;BH=x,则BD=2x,BF=2x-2,利用勾股定理可得![]() ,
,![]() ;解得BH=
;解得BH=![]() ,AB=BH+AH=
,AB=BH+AH=![]() ,由AO=
,由AO=![]() AB=
AB=![]() ,即可得⊙
,即可得⊙![]() 的半径.
的半径.
(1)证明:∵AB为⊙![]() 直径,
直径,
∴![]() =90°,
=90°,
∴![]() °,
°,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() °,
°,
即![]() °,
°,
∴AC为⊙![]() 的切线;
的切线;
(2)证明:∵![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() ;
;
∴![]() ,
,
∵![]() ,
,
∴![]() ;
;
即AE平分![]() .
.
(3)解:过点F作FH⊥AB于H.

∴![]() °;
°;
又∵![]() ,AF=AF,
,AF=AF,
∴![]() ;
;
∴AH=AD=4,FH=DF=2;
∵![]() °,
°,![]() ,
,
∴![]() ,
,
∴![]() ;
;
设BH=x,则BD=2x,BF=2x-2,
∴![]() ,
,
∴![]() ;
;
∴x=0(舍)或x=![]() ;
;
∴BH=![]() ,AB=BH+AH=
,AB=BH+AH=![]() ;
;
∴AO=![]() AB=
AB=![]() ;
;
∴⊙![]() 的半径为
的半径为![]() .
.


科目:初中数学 来源: 题型:
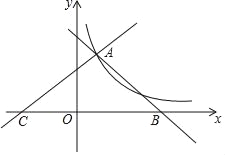
【题目】如图,直线y1=﹣x+4,y2=![]() x+b都与双曲线y=
x+b都与双曲线y=![]() 交于点A(1,m),这两条直线分别与x轴交于B,C两点.
交于点A(1,m),这两条直线分别与x轴交于B,C两点.
(1)求y与x之间的函数关系式;
(2)直接写出当x>0时,不等式![]() x+b>
x+b>![]() 的解集;
的解集;
(3)若点P在x轴上,连接AP把△ABC的面积分成1:3两部分,求此时点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点![]() 在正方形
在正方形![]() 的对角线
的对角线![]() 上,正方形
上,正方形![]() 的边长是
的边长是![]() ,
,![]() 的两条直角边
的两条直角边![]() 分别交边
分别交边![]() 于点
于点![]() .
.
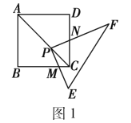
(1)操作发现:如图2,固定点![]() ,使
,使![]() 绕点
绕点![]() 旋转,当
旋转,当![]() 时,四边形
时,四边形![]() 是正方形.
是正方形.
填空:①当![]() 时,四边形
时,四边形![]() 的边长是_____;
的边长是_____;
②当![]() (
(![]() 是正实数)时,四边形
是正实数)时,四边形![]() 的面积是______;
的面积是______;
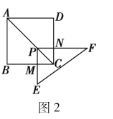
(2)猜想论证:如图3,将四边形![]() 的形状改变为矩形,
的形状改变为矩形,![]() ,
,![]() ,点
,点![]() 在矩形
在矩形![]() 的对角线
的对角线![]() ,
,![]() 的两条直角边
的两条直角边![]() 分别交边
分别交边![]() 于点
于点![]() ,固定点
,固定点![]() ,使
,使![]() 绕点
绕点![]() 旋转,则
旋转,则![]() ______;
______;
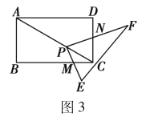
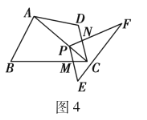
(3)拓展探究:如图4,当四边形![]() 满足条件:
满足条件:![]() ,
,![]() ,时,点
,时,点![]() 在对角线
在对角线![]() 上,
上,![]() 分别交边
分别交边![]() 于点
于点![]() ,固定点
,固定点![]() ,使
,使![]() 绕点
绕点![]() 旋转,请探究
旋转,请探究![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】外线投篮是篮球队常规训练的重要项目之一,下列图表中数据是甲、乙、丙三人每人十次投篮测试的成绩.测试规则为连续投篮十个球为一次,投进篮筐一个球记为1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
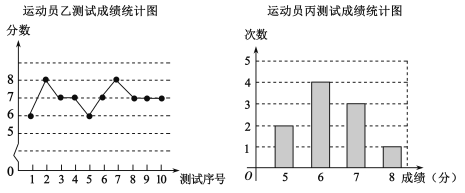
(1)写出运动员乙测试成绩的众数和中位数;
(2)在他们三人中选择一位投篮成绩优秀且较为稳定的选手作为中锋,你认为选谁更合适?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 的最高点的纵坐标是2.
的最高点的纵坐标是2.

(1)求抛物线的表达式;
(2)将抛物线在![]() 之间的部分记为图象
之间的部分记为图象![]() ,将图象
,将图象![]() 沿直线x=1翻折,翻折后图象记为
沿直线x=1翻折,翻折后图象记为![]() ,图象
,图象![]() 和
和![]() 组成G,直线
组成G,直线![]() :
:![]()
![]() 和图象G在x轴上方的部分有两个公共点,求k的取值范围;
和图象G在x轴上方的部分有两个公共点,求k的取值范围;
(3)直线![]() :
:![]() 与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求
与图象G在x轴上方的部分分别交于A、M、P、Q四点,若AM=2PQ,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() ,把
,把![]() 的各边进行下列变换:①各边的长度分别扩大为原来的3倍;②各边的长度分别缩小为原来的
的各边进行下列变换:①各边的长度分别扩大为原来的3倍;②各边的长度分别缩小为原来的![]() ;③各边的长度分别增加2;④各边的长度分别平方.其中得到的三角形与
;③各边的长度分别增加2;④各边的长度分别平方.其中得到的三角形与![]() 相似的有( )
相似的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
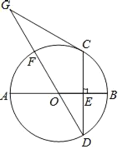
(1)判断CG与圆O的关系,并说明理由;
(2)若CD=6,求线段GF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
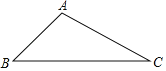
【题目】超速行驶被称为“马路第一杀手”为了让驾驶员自觉遵守交通规则,湖浔大道公路检测中心在一事故多发地段安装了一个测速仪器,如图所示,已知检测点设在距离公路10米的A处,测得一辆汽车从B处行驶到C处所用时间为1.35秒.已知∠B=45°,∠C=30°.
(1)求B,C之间的距离(结果保留根号);
(2)如果此地限速为70km/h,那么这辆汽车是否超速?请说明理由.(参考数据;![]() ≈1.7,
≈1.7,![]() ≈1.4)
≈1.4)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的袋子中装有红、白两种颜色的小球,这些球除颜色外完全相同,其中红球1个,若从中随机摸出一个球,这个球是白球的概率为![]()
(1)求袋子中白球的个数
(2)随机摸出一个球后,放回并搅匀,再随机摸出一个球,请用画树状图或列表的方法,求两次都摸到白球的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com