
【题目】如图①,直线y= ![]() x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
x+4交于x轴于点A,交y轴于点C,过A、C两点的抛物线F1交x轴于另一点B(1,0).
(1)求抛物线F1所表示的二次函数的表达式;
(2)若点M是抛物线F1位于第二象限图象上的一点,设四边形MAOC和△BOC的面积分别为S四边形MAOC和S△BOC , 记S=S四边形MAOC﹣S△BOC , 求S最大时点M的坐标及S的最大值;
(3)如图②,将抛物线F1沿y轴翻折并“复制”得到抛物线F2 , 点A、B与(2)中所求的点M的对应点分别为A′、B′、M′,过点M′作M′E⊥x轴于点E,交直线A′C于点D,在x轴上是否存在点P,使得以A′、D、P为顶点的三角形与△AB′C相似?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:令y=0代入y= ![]() x+4,
x+4,
∴x=﹣3,A(﹣3,0),
令x=0,代入y= ![]() x+4,∴y=4,∴C(0,4),
x+4,∴y=4,∴C(0,4),
设抛物线F1的解析式为:y=a(x+3)(x﹣1),
把C(0,4)代入上式得,a=﹣ ![]() ,
,
∴y=﹣ ![]() x2﹣
x2﹣ ![]() x+4
x+4
(2)
解:如图1
 ,
,
设点M(a,﹣ ![]() a2﹣
a2﹣ ![]() a+4),其中﹣3<a<0
a+4),其中﹣3<a<0
∵B(1,0),C(0,4),
∴OB=1,OC=4
∴S△BOC= ![]() OBOC=2,
OBOC=2,
过点M作MD⊥x轴于点D,
∴MD=﹣ ![]() a2﹣
a2﹣ ![]() a+4,AD=a+3,OD=﹣a,
a+4,AD=a+3,OD=﹣a,
∴S四边形MAOC= ![]() ADMD+
ADMD+ ![]() (MD+OC)OD
(MD+OC)OD
= ![]() ADMD+
ADMD+ ![]() ODMD+
ODMD+ ![]() ODOC
ODOC
= ![]() MD(AD+OD)+
MD(AD+OD)+ ![]() ODOC
ODOC
= ![]() MDOA+
MDOA+ ![]() ODOC
ODOC
= ![]() ×3(﹣
×3(﹣ ![]() a2﹣
a2﹣ ![]() a+4)+
a+4)+ ![]() ×4×(﹣a)
×4×(﹣a)
=﹣2a2﹣6a+6
∴SS四边形MAOC﹣S△BOC
=(﹣2a2﹣6a+6)﹣2
=﹣2a2﹣6a+4
=﹣2(a+ ![]() )2+
)2+ ![]()
∴当a=﹣ ![]() 时,S有最大值,最大值为
时,S有最大值,最大值为 ![]() ,此时,M(﹣
,此时,M(﹣ ![]() ,5)
,5)
(3)
解:如图2
 ,
,
由题意知:M′( ![]() ,5),B′(﹣1,0),A′(3,0),
,5),B′(﹣1,0),A′(3,0),
∴AB′=2
设直线A′C的解析式为:y=kx+b,把A′(3,0)和C(0,4)代入y=kx+b,
得: ![]() ,
,
∴ 
∴y=﹣ ![]() x+4,
x+4,
令x= ![]() 代入y=﹣
代入y=﹣ ![]() x+4,
x+4,
∴y=2,∴D( ![]() ,2)
,2)
由勾股定理分别可求得:AC=5,DA′= ![]()
设P(m,0),当m<3时,此时点P在A′的左边,
∴∠DA′P=∠CAB′,
当 ![]() =
= ![]() 时,△DA′P∽△CAB′,此时,
时,△DA′P∽△CAB′,此时, ![]() =
= ![]() (3﹣m),
(3﹣m),
解得:m=2,
∴P(2,0)
当 ![]() =
= ![]() 时,△DA′P∽△B′AC,此时,
时,△DA′P∽△B′AC,此时, ![]() =
= ![]() (3﹣m)
(3﹣m)
m=﹣ ![]() ,
,
∴P(﹣ ![]() ,0)
,0)
当m>3时,此时,点P在A′右边,由于∠CB′O≠∠DA′E,
∴∠AB′C≠∠DA′P,
∴此情况,△DA′P与△B′AC不能相似,
综上所述,当以A′、D、P为顶点的三角形与△AB′C相似时,点P的坐标为(2,0)或(﹣ ![]() ,0)
,0)
【解析】(1)根据自变量与函数值得对应关系,可得A.C点坐标,根据待定系数法,可得答案;(2)根据面积的和差,可得二次函数,根据二次函数的性质,可得答案;(3)根据待定系数法,可得函数解析式,根据相似三角形的性质,可得关于m的方程,根据解方程,可得答案.
【考点精析】通过灵活运用确定一次函数的表达式和相似三角形的性质,掌握确定一个一次函数,需要确定一次函数定义式y=kx+b(k不等于0)中的常数k和b.解这类问题的一般方法是待定系数法;对应角相等,对应边成比例的两个三角形叫做相似三角形即可以解答此题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案 能考试全能100分系列答案
能考试全能100分系列答案科目:初中数学 来源: 题型:
【题目】阅读下面材料后,解答问题。
分母中含有未知数的不等式叫分式不等式。如:![]() ;
;![]() 等。那么如何求出它们的解集呢?
等。那么如何求出它们的解集呢?
根据我们学过的有理数除法法则可知:两数相除,同号得正,异号得负,其字母表达式为:
(1)若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]() ;
;
(2)若![]() ,
,![]() ,则
,则![]() ;若
;若![]() ,
,![]() ,则
,则![]() .
.
请解答下列问题:
(1)反之:①若![]() 则
则![]() 或
或![]() ;②若
;②若![]() ,则__________;
,则__________;
(2)根据上述规律,求不等式![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
12×231=132×21, 14×451=154×41, 32×253=352×23, 34×473=374×43,45×594=495×54,……
以上每个等式中两边数字是分别对称的,且每个等式中组成两位数与三位数的数字之间具有相同规律,我们称这类等式为“数字对称等式”.
(1)根据上述各式反映的规律填空,使式子成为“数字对称等式”:
①35× = ×53; ② ×682=286× .
(2)设数字对称式左边的两位数的十位数字为m,个位数字为n,且2≤m+n≤9.用含m,n的代数式表示数字对称式左边的两位数与三位数的乘积P,并求出P 能被110整除时mn的值.(其中乘法公式![]() ))
))
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年《政府工作报告》中提出了十大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的A:“互联网+政务服务”,B:“工匠精神”,C:“光网城市”,D:“大众旅游时代”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词.根据调查结果,该小组绘制了如下的两幅不完整的统计图. 
请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中,m= , n=;
(3)扇形统计图中,热词B所在扇形的圆心角是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠BAC的平分线交BC于点D,DE⊥AD,交AB于点E,AE为⊙O的直径 
(1)判断BC与⊙O的位置关系,并证明你的结论;
(2)求证:△ABD∽△DBE;
(3)若cosB= ![]() ,AE=4,求CD.
,AE=4,求CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )

A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
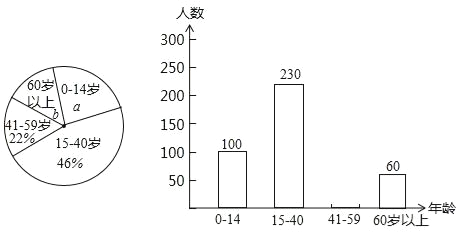
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重阳节期间,某单位组织本单位退休职工前去距离商丘480千米的信阳鸡公山登高旅游,由于人数较多,共租用甲、乙两辆长途汽车沿同一路线赶赴景点.图中的折线、线段分别表示甲、乙两车所走的路程y甲(千米),y乙(千米)与时间x(小时)之间的函数关系对应的图象.请根据图象所提供的信息,解决下列问题: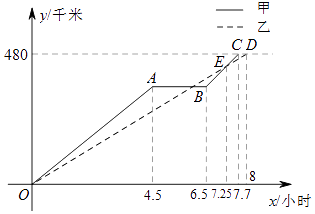
(1)由于汽车发生故障,甲车在途中停留了小时;
(2)甲车排除故障后,立即提速赶往景点.请问甲车在排除故障时,距出发点的路程是多少千米?
(3)为了保证及时联络,甲、乙车在第一次相遇时约定此后两车之间的路程不超过35千米,请通过计算说明,按图象所表示的走法是否符合约定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥EF,则∠A、∠C、∠D、∠E满足的数量关系是( )

A. ∠A+∠C+∠D+∠E=360°
B. ∠A+∠D=∠C+∠E
C. ∠A-∠C+∠D+∠E=180°
D. ∠E-∠C+∠D-∠A=90°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com