
【题目】已知图甲是一个长为![]() ,宽为
,宽为![]() 的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
的长方形,沿图甲中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
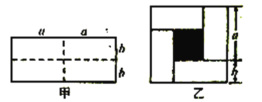
(1)求图乙中阴影部分正方形的边长(用含字母![]() ,
,![]() 的整式表示);
的整式表示);
(2)请用两种不同的方法求图乙中阴影部分的面积.
(3)观察图乙,并结合(2)中的结论,写出下列三个整式:![]() ,
,![]() ,
,![]() 之间的等量关系;
之间的等量关系;
(4)根据(3)题中的等量关系,解决如下问题:若![]() ,
,![]() ,求
,求![]() 的值.
的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某条公共汽车线路收支差额![]() 与乘客量
与乘客量![]() 的函数关系如图所示(收支差额
的函数关系如图所示(收支差额![]() 车票收入
车票收入![]() 支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
支出费用),由于目前本条线路亏损,公司有关人员提出了两条建议:建议(Ⅰ)不改变支出费用,提高车票价格;建议(Ⅱ)不改变车票价格,减少支出费用. 下面给出的四个图形中,实线和虚线分别表示目前和建议后的函数关系,则( )
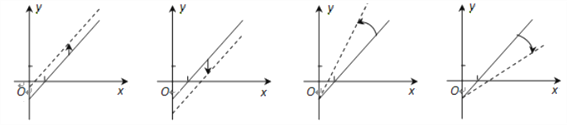
④ ③ ② ①
A. ①反映了建议(Ⅰ),③反映了建议(Ⅱ) B. ②反映了建议(Ⅰ),④反映了建议(Ⅱ)
C. ①反映了建议(Ⅱ),③反映了建议(Ⅰ) D. ②反映了建议(Ⅱ),④反映了建议(Ⅰ)
查看答案和解析>>
科目:初中数学 来源: 题型:
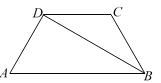
【题目】已知:如图,在梯形ABCD中,DC∥AB,AD=BC,BD平分∠ABC,∠A=60°.
求:(1)求∠CDB的度数;
(2)当AD=2时,求对角线BD的长和梯形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上线段AB=2(单位长度),CD=4(单位长度),点A在数轴上表示的数是﹣8,点C 在数轴上表示的数是10.若线段AB以6个单位长度/秒的速度向右匀速运动,同时线段CD以2个单位长度/秒的速度也向右匀速运动.
![]()
(1)运动t秒后,点B表示的数是 ;点C表示的数是 .(用含有t的代数式表示)
(2)求运动多少秒后,BC=4(单位长度);
(3)P是线段AB上一点,当B点运动到线段CD上时,是否存在关系式![]() ,若存在,求线段PD的长;若不存在,请说明理由.
,若存在,求线段PD的长;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
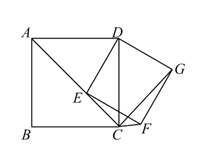
【题目】如图,已知四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG。
(1)求证:矩形DEFG是正方形。
(2)当点E从A点运动到C点时;
①求证:∠DCG的大小始终不变;
②若正方形ABCD的边长为2,则点G运动的路径长为 。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式(组):
(Ⅰ)解不等式:![]() <
<![]()
(Ⅱ)解不等式组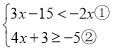
请结合题意填空,完成本题的解答;
(1)解不等式①,得: ;
(2)解不等式②,得: ;
(3)把不等式①和②的解集在如图数轴上表示出来;
![]()
(4)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
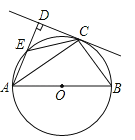
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD与过点C的切线互相垂直,垂足为点D,AD交⊙O于点E,连接CE,CB.
(1)求证:CE=CB;
(2)若AC=![]() ,CE=
,CE=![]() ,求AE的长.
,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
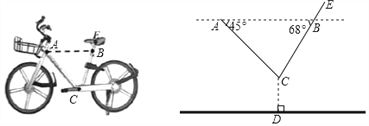
【题目】如图,一辆摩拜单车放在水平的地面上,车把头下方A处与坐垫下方B处在平行于地面的水平线上,A、B之间的距离约为49cm,现测得AC、BC与AB的夹角分别为45°与68°,若点C到地面的距离CD为28cm,坐垫中轴E处与点B的距离BE为4cm,求点E到地面的距离(结果保留一位小数).(参考数据:sin68°≈0.93,cos68°≈0.37,cot68°≈0.40)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:![]() 是最大的负整数,且
是最大的负整数,且![]() 、b、c满足(c﹣5)2+|
、b、c满足(c﹣5)2+|![]() +b|=0,请回答问题.
+b|=0,请回答问题.
![]()
(1)请直接写出![]() 、b、c的值:
、b、c的值:![]() = ,b= ,c= .
= ,b= ,c= .
(2)![]() 、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
、b、c所对应的点分别为A、B、C,点P为一动点,其对应的数为x,点P在0到1之间运动时(即0 ≤ x ≤ 1时),请化简式子:|x+1|﹣|x﹣1|+2|x-5|(请写出化简过程).
(3)在(1)(2)的条件下,点A、B、C开始在数轴上运动,若点A以每秒2个单位长度的速度向左运动,同时,点B和点C分别以每秒3个单位长度和8个单位长度的速度向右运动,假设t秒钟过后,若点B与点C之间的距离表示为BC,点A与点B之间的距离表示为AB.请问:BC﹣AB的值是否随着时间t的变化而改变?若变化,请说明理由;若不变,请求其值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com