
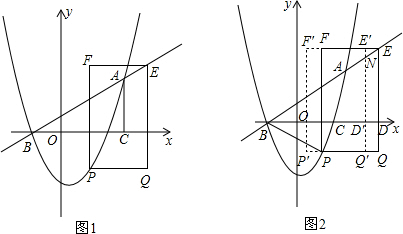
分析 (1)用待定系数法求出抛物线和直线的解析式,
(2)先确定出要使周长最大,EQ最大即可,求出EQ函数关系式即可;
(3)①N在线段AE上时QJ=$\frac{18}{7}$,IP=$\frac{9}{2}$,再求出面积S=S梯形+S△IDA,②N在AB上时,MQ=2,NK=1在计算面积即可S=S梯形MQPI+S梯形PKNI
解答 解:∵B的坐标为(-2,0)直线y=mx+n过点B和抛物线上另一点A(4,3),
∴$\left\{\begin{array}{l}{-2m+n=0}\\{4m+n=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=1}\end{array}\right.$,
∴直线解析式为y=$\frac{1}{2}$x+1,
∵抛物线过点A,B,
∴$\left\{\begin{array}{l}{4a-2b-3=0}\\{16a+4b-3=3}\end{array}\right.$,
∴$\left\{\begin{array}{l}{a=\frac{1}{2}}\\{b=-\frac{1}{2}}\end{array}\right.$,
∴y=$\frac{1}{2}$x2-$\frac{1}{2}$x-3,
(2)由矩形的周长为2(PQ+EQ)=8+2EQ,要使周长最大,EQ最大即可,
设P(a,$\frac{1}{2}$a2-$\frac{1}{2}$a-3),
∴Q(a+4,$\frac{1}{2}$a2-$\frac{1}{2}$a-3),E(a+4,$\frac{1}{2}$a+3),
∴EQ=$\frac{1}{2}$a+3-($\frac{1}{2}$a2-$\frac{1}{2}$a-3)=-$\frac{1}{2}$(a-1)2+$\frac{13}{2}$,
∴当a=1时,EQ最大,P(1,-3),
(3)如图2,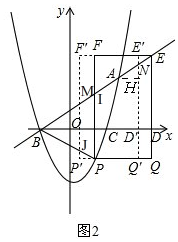
①N在线段AE上时,有DD′=t,OD′=5-t,D′(5-t,0),N(5-t,-$\frac{1}{2}$t+$\frac{7}{2}$),
过点A作AH⊥ND′,
∴AH∥x轴,
∴NH=-$\frac{1}{2}$t+$\frac{7}{2}$-3=-$\frac{1}{2}$t+$\frac{1}{2}$,
∴M(0,1)
∴OM=1,
∴BM=$\sqrt{5}$,
∴sin∠MBO=$\frac{1}{\sqrt{5}}$,
∵AH∥x轴,
∴∠NAH=∠MBO,
∴sin∠MBO=$\frac{1}{\sqrt{5}}$,
∴$\frac{NH}{NA}=\frac{1}{\sqrt{5}}$,
∴NA=$\sqrt{5}$(-$\frac{1}{2}$t+$\frac{1}{2}$)
由NA=$\frac{\sqrt{5}}{8}$ND′
∴$\sqrt{5}$(-$\frac{1}{2}$t+$\frac{1}{2}$)=$\frac{\sqrt{5}}{8}$(-$\frac{1}{2}$t+$\frac{7}{2}$),
∴t=$\frac{1}{7}$,
∵BP的解析式为y=-x-2,
xJ=$\frac{6}{7}$,yJ=-$\frac{20}{7}$,
∴J($\frac{6}{7}$,-$\frac{20}{7}$),
∵M($\frac{6}{7}$,$\frac{10}{7}$),
∴MJ=$\frac{30}{7}$,
同理:IP=$\frac{9}{2}$,
∴S=S梯形+S△IPA=$\frac{103}{14}$,
②N在AB上时,同①的方法一样,S=$\frac{1}{2}$×(2+$\frac{9}{2}$)×$\frac{5}{3}$+$\frac{1}{2}$(1+$\frac{9}{2}$)×($\frac{10}{3}$-1)=$\frac{49}{6}$
点评 此题是二次函数综合题,主要考查了待定系数法求函数解析式,三角形面积的计算,锐角三角函数,平面坐标系中线段的求法,解本题的关键是用平面坐标系中两点间的距离公式计算线段,难点是表示出点的坐标.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 由a>b得-2a>-2b | B. | 由-1>-2得$\frac{1}{\sqrt{2}}$>$\frac{2}{\sqrt{2}}$ | C. | 由a>b得ac>bc | D. | 由a>b得-a<-b |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一个靶子如图所示,已知中心10环的半径r=10cm,9环的半径R1=20cm,8环的半径R2=40cm,如果每发子弹都打在靶上并取得环数.
一个靶子如图所示,已知中心10环的半径r=10cm,9环的半径R1=20cm,8环的半径R2=40cm,如果每发子弹都打在靶上并取得环数.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
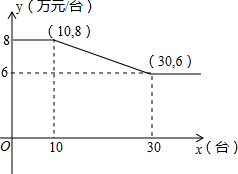 某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.
某公司销售智能机器人,售价每台为10万元,进价y与销售量x的函数关系式如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com