
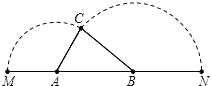
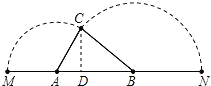
 点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
|
| 5 |
| 3 |
| 4 |
| 3 |
| 5 |
| 3 |
| 4 |
| 3 |
| 1 |
| 2 |
| 1-h2 |
| (3-x)2-h2 |
| 1-h2 |
| 1-h2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
| 4 |
| 3 |
| 1 |
| 2 |
| ||
| 2 |
| (3-x)2-h2 |
| 1-h2 |
| 1 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 4 |
| 3 |
| ||
| 2 |
| ||
| 2 |


 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
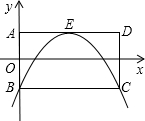 平面直角坐标系.
平面直角坐标系.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
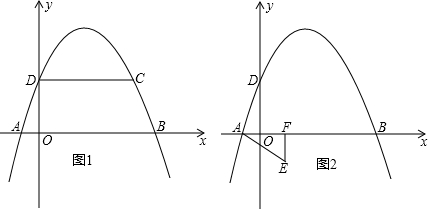
科目:初中数学 来源:不详 题型:解答题
 F沿直线EF折叠,点P的对应点为P′,请直接写出P′点坐标,并判断点P′是否在该抛物线上.
F沿直线EF折叠,点P的对应点为P′,请直接写出P′点坐标,并判断点P′是否在该抛物线上.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
| 1 |
| 12 |
| 2 |
| 3 |
| 5 |
| 3 |

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com