
【题目】如图,C,D为线段AB上的两点,M,N分别是线段AC,BD的中点.
(1)如果CD=5cm,MN=8cm,求AB的长;
(2)如果AB=a,MN=b,求CD的长.
![]()
【答案】(1)线段AB的长为11cm;(2)2b﹣a.
【解析】
(1)先根据M,N分别是线段AC,BD的中点,可得MC=![]() AC,DN=
AC,DN=![]() BD,
BD,
再根据MC+CD+DN=MN=8cm,可得MC+DN=8﹣5=3cm,进而可得:AC+BD=2MC+2DN=2×3=6cm,所以AB=AC+CD+BD=AC+BD+CD=6+5=11(cm),
(2)根据M,N分别是线段AC,BD的中点,可得CM=AM=![]() AC,BN=DN=
AC,BN=DN=![]() BD,
BD,
再根据AM+BN=MC+DN=AB﹣MN,可得MC+DN=a﹣b,
进而可得:CD=MN﹣(MC+DN)=b﹣(a﹣b)=2b﹣a.
(1)M,N分别是线段AC,BD的中点,
∴MC=![]() AC,DN=
AC,DN=![]() BD,
BD,
∵MC+CD+DN=MN=8cm,
∴MC+DN=8﹣5=3cm,
∴AC+BD=2MC+2DN=2×3=6cm,
∴AB=AC+CD+BD=AC+BD+CD=6+5=11(cm),
即线段AB的长为11cm,
(2)M,N分别是线段AC,BD的中点,
∴CM=AM=![]() AC,BN=DN=
AC,BN=DN=![]() BD,
BD,
∵AM+BN=MC+DN=AB﹣MN,
∴MC+DN=a﹣b,
∴CD=MN﹣(MC+DN)=b﹣(a﹣b)=2b﹣a.


科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b(k<0)与反比例函数y= ![]() 的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1)
的图象相交于A、B两点,一次函数的图象与y轴相交于点C,已知点A(4,1) 
(1)求反比例函数的解析式;
(2)连接OB(O是坐标原点),若△BOC的面积为3,求该一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
6 | a | b | x | -2 | 1 | … |
(1)可求得x=______,第2016个格子中的数为______;
(2)判断:前m个格子中所填整数之和是否可能为2016?若能,求出m的值,若不可能,请说明理由;
(3)如果x,y为前3格子中的任意两个数,那么所有的|x-y|的和可以通过计算|6-a|+|a-6|+|a-b|+|b-a|+|6-b|+|b-6|得到.若x,y为前20格子中的任意两个数,则所有的|a-b|的和为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,已知△ABC的三个顶点的坐标分别为A(﹣2,3),B(﹣6,0),C(﹣1,0).

(1)请直接写出点B关于点A对称的点的坐标;
(2)将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;
(3)请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(6分)下面是小马虎解的一道题
题目:在同一平面上,若∠BOA=70°,∠BOC=15°求∠AOC的度数.
解:根据题意可画出图,

∵∠AOC=∠BOA-∠BOC
=70°-15°
=55°,
∴∠AOC=55°.
若你是老师,会判小马虎满分吗?若会,说明理由.若不会,请将小马虎的的错误指出,并给出你认为正确的解法.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店在甲批发市场以每包m元的价格进了40包茶叶,又在乙批发市场以每包n元(m>n)的价格进了同样的60包茶叶,如果商家以每包![]() 元的价格卖出这种茶叶,卖完后,这家商店( )
元的价格卖出这种茶叶,卖完后,这家商店( )
A.盈利了 B.亏损了 C.不赢不亏 D.盈亏不能确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线x= ![]() 的抛物线经过点A(6,0)和B(0,﹣4).
的抛物线经过点A(6,0)和B(0,﹣4). 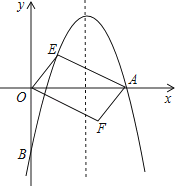
(1)求抛物线解析式及顶点坐标;
(2)设点E(x,y)是抛物线上一动点,且位于第一象限,四边形OEAF是以OA为对角线的平行四边形,求平行四边形OEAF的面积S与x之间的函数关系式;
(3)当(2)中的平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知点A、B的坐标分别为(8,0)、(0,2 ![]() ),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为
),C是AB的中点,过点C作y轴的垂线,垂足为D,动点P从点D出发,沿DC向点C匀速运动,过点P作x轴的垂线,垂足为E,连接BP、EC.当BP所在直线与EC所在直线第一次垂直时,点P的坐标为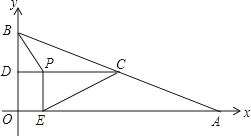
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面题目的解题过程,并回答问题.
若![]() ,求x2+y2的值.
,求x2+y2的值.
解:设![]() ,则原式可化为a2-8a+16=0,即(a-4)2=0,所以a=4.
,则原式可化为a2-8a+16=0,即(a-4)2=0,所以a=4.
由(x2+y2)2=4,得x2+y2=±2.
(1)错误的原因是___________________________________
(2)本题正确的结论为_________________________________
(3)设“![]() ”的方法叫做换元法,它能起到化繁为简的目的.请用“换元法”把(x+y)2-14(x+y)+49因式分解.
”的方法叫做换元法,它能起到化繁为简的目的.请用“换元法”把(x+y)2-14(x+y)+49因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com