
如图所示,在⊙O中,半径OB⊥OE于O点,C是OE延长线上一点,过C点作CA切⊙O于A点,连接AB交OE于D点,求证:CA=CD.
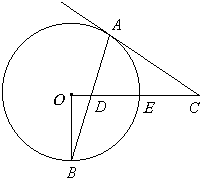
|
证法一:连接 OA,
∵AC是切线, ∴∠OAC=90°,即∠OAD=∠DAC=90° ∵OB⊥OE,∴∠DOB=90°. ∴∠B+∠ODB=90°,即∠B+∠ADC=90°. ∴∠OAD+∠DAC=∠B+∠ADC. ∵OA=OB,∴∠B=∠OAD. ∴∠DAC=∠ADC,∴CA=CD. 证法二:延长BO交⊙O于F点. ∵FB是直径,∴∠FAD=90°. ∵BO⊥OE,∴∠FOD=90°.∴∠F+∠ADO=180°, ∵∠ODA+∠ADC=180°,∴∠F=∠ADC. ∵AC是切线, ∴∠DAC=∠F.∴∠DAC=∠ADC.∴CA=CD. 证法三:连接AE、BE. ∵AC是切线,∴∠CAE=∠DBE. ∵OB=OE且BO⊥OE,∴∠OEB=45°. ∵∠BAE=45°, ∴∠BAE=∠DEB. ∵∠ADC=∠DBE+∠DEB,且∠DAC=∠DAE+∠EAC,∴∠ADC=∠DAC,∴CA=CD. |
|
由于所证两条线段交于点 C,且CA是切线长,CD既不是切线也不是弦,因此无法直接证明,这时只有转化关系,寻求角的关系了.考虑到存在∠BOC=90°,且∠ADC与之相关,因此只有把∠DAC也放到直角三角形中才能沟通关系;从另一个角度考虑,有切线必然存在弦切角,这时利用不同的弦切角沟通关系也可构成不同的证明方法. |


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:
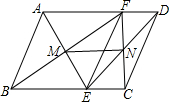 如图所示,在?ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF交于点M,连接CF,DE交于点N,求证:MN∥AD且MN=
如图所示,在?ABCD中,EF∥AB且交BC于点E,交AD于点F,连接AE,BF交于点M,连接CF,DE交于点N,求证:MN∥AD且MN=| 1 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com